science-review.ru
Определение сложности вычислений актуально в связи с моделированием технологических, научных и социальных процессов и активным развитием искусственного интеллекта [1, 2]. Поэтому практически важно установление оценок сложности вычисления в зависимости от особенностей предметной области, над которой вычисление осуществляется [3, 4]. В статье рассматриваются арифметические двоичные программы над полным базисом v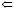 
v + 1, v 
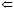0, v = u операторов, обозначаемые соответственно s(x), 0(x), E(v, u). Каждая программа представляется орграфом с арифметическими вершинами s(x), 0(x) и логическими (E), обладает одной входной переменной x и конечным набором y1, y2, ..., ym рабочих, среди которых одна – выходная. При этом одна вершина – входная; одна – выходная; в арифметических вершинах используются только рабочие переменные; в логических могут использоваться как рабочие, так и входная. Все определения, необходимые для детального понимания содержания статьи, приведены в [5]. В силу ограниченного объема статьи здесь приведены лишь пояснения к некоторым определениям, чтобы сделать изложение понятнее.
Пусть t = n1, n2, …, nl – путь в программе p. Заменим каждый его предикат P(z1, z2) предикатом Ps(z1, z2), где s ∈ {0, 1} так, что следующая в t за P(z1, z2) вершина является его s-последователем. Полученную последовательность назовем размеченным путем и обозначим t. Содержательно размеченный путь представляет вычисление в программе. Если он начинается во входной вершине и заканчивается в выходной, то он представляет полное вычисление программы.
Рассуждения в настоящей статье базируются на результате Ю.И. Янова (Проблемы кибернетики, вып. 32), который показал, что каждую арифметическую программу можно представить в виде конечного автомата, состояния которого суть логические и заключительная вершины, а входной алфавит образован следующими «буквами». Если из логической вершины E в логическую вершину E1 ведет путь E, n1, n2, …, nl, E1, где n1 есть s-последователь вершины E, n1, n2, …, nl суть арифметические вершины и l ≥ 0, то переход из состояния E в состояние E1 происходит под воздействием автоматной буквы Es, n1, n2, …, nl . Представимое таким автоматом событие состоит из всех полных размеченных путей программы. Регулярное выражение Rp, представляющее множество всех полных путей, представимо в виде суммы R1 ∨ R2 ∨…∨ Rr членов, не содержащих операции суммирования. Очевидно, что каждое выражение Ri, i = 1, 2, …, r представляет только полные вычисления, а всякое его регулярное подвыражение определяет совокупность целочисленных функций.
В [5] показано, как по регулярному выражению R1 ∨ R2 ∨…∨ Rr построить обобщенную логическую формулу, представляющую функцию, вычисляемую программой p. Построение основывается на том, что все базисные операторы представимы обобщенными формулами. Построенная формула вместо переменных содержит так называемые метапеременные, которые устанавливают соответствие между этой формулой и вычислениями. Дальнейшее содержание статьи состоит в исследовании свойств этой формулы.
Цель статьи состоит в установлении длины вычисления программы в зависимости от свойств предметной области, над которой вычисляется программа.
Соотношение обобщенных формул, регулярных выражений и размеченных путей
Построим обобщенную ДНФ (ОДНФ) по формуле, представляющей функцию, определяемой регулярным выражением Rp. Для этого отметим, что каждое регулярное выражение A* определяет бесконечную дизъюнкцию. Если A не содержит оператора *, то соответствующая формула уже представлена в ОДНФ, с бесконечным числом конъюнктов, каждый из которых обладает конечной длиной. Если выражение A содержит оператор *, то индукцией по числу операторов * показывается, что определяемое им выражение эквивалентно преобразуется в бесконечную дизъюнкцию конъюнктов конечной длины, атомарными формулами в которых служат формулы 0, S и E. Эту дизъюнкцию назовем обобщенной ДНФ.
Установим соответствие между ОДНФ и вычислениями программы, определяемыми размеченными путями. Индукцией по длине регулярного выражения доказывается теорема.
Теорема 1. Пусть формула F определяется регулярным выражением. Тогда по ней единственным образом строится ОДНФ, в которой каждый конъюнкт представляет в точности одну функцию, определяемую единственным размеченным путем программы.
Будем исследовать так называемые частичные вычисления, которые определяются означиванием лишь конечного префикса входной переменной программы. В результате такого означивания sx программа p(x) превращается в новую программу p', а первоначальная формула F, построенная по регулярному выражению Rp, в новую формулу F', представляющую функцию, вычисляемую программой p'. Преобразование формулы F в F' базируется на следующих эквивалентных преобразованиях.
Пусть обобщенная формула G построена по регулярному выражению. Введем так называемое правильное означивание метапеременных формулы G. Допустим, что означен некоторый префикс входной переменной, а рабочие метапеременные означиваются следующим образом.
1. Если в G встречается формула 0(a), где a = a0, …, am …, то a0 = … = am = … = 0. Очевидно, это единственное означивание метапеременных, при котором формула 0(a) истинная.
2. Если в G встречается формула Sl(a, b), a = a0, …, am, …, b = b0, …, bm, …, то a, b – рабочие метапеременные. Следовательно, имеется самая правая единица в означивании компонентов a0, …, am, …, за которой следуют бесконечный нулевой суффикс. Тогда означивание компонентов b0, …, bm, … получается из двоичного представления числа |a| + l. Здесь |a| – это двоичное число, определяемое значениями метапеременных a0, …, am, … отбрасыванием бесконечного нулевого суффикса правее последнего единичного компонента. При таком означивании метапеременных a, b формула Sl истинная, при любом другом означивании метапеременных b0, …, bm, … она ложна.
3. Если a и b суть рабочие метапеременные, то формула E(a, b) истинная при означиваниях, соответственно σa и σb лишь в случае, когда σa = σb, т.е. σa и σb суть равные двоичные числа. А формула E-1(a, b) истинная лишь в случае, когда σa ≠ σb, т.е. σa и σb суть равные двоичные числа.
Пусть G(a1, a2, …, aq) есть конъюнкция формул, представляющих арифметические и логические операторы, содержащая только рабочие метапеременные a1, a2, …, aq. Тогда при означивании ее метапеременных она истинная тогда и только тогда, когда означивания правильные, т.е. удовлетворяют условиям из пунктов 1–3. Если конъюнкция G построена по регулярному выражению, определяемому размеченным путем, то значения ее метапеременных полностью соответствуют вычисленным значениям рабочих переменных. То есть вычисление, определяемое размеченным путем, совпадает с правильным означиванием, и наоборот, всякое правильное означивание совпадает с вычислением, определяемым размеченным путем. Такой вывод справедлив лишь при условии, когда размеченный путь не включает логической вершины, содержащей входную переменную программы. Рассмотрим, что происходит, если в размеченном пути встречаются логические операторы, содержащие входную переменную программы. Легко показать, что формула E(a, b) может быть либо ложной, либо неопределенной, а E-1(a, b) – либо истинной либо неопределенной. Формула Es(a, b) после означивания ее метапеременных представляет собой конъюнкт или дизъюнкт литер, лишь когда она содержит частично означенную входную переменную и означенные префиксы метапеременных a и b совпадают. Таким образом, если логический оператор не содержит частично означенной переменной, то его логическое значение совпадает с логическим значением представляющей формулы. Но если логический оператор содержит частично означенную входную переменную, то не является константой, и его окончательное значение зависит от дальнейшего означивания входной переменной.
Расширение означивания префикса входной переменной программы
Естественно возникает вопрос, что происходит с формулой, которая строится по регулярному выражению Rp, если расширяется означиваемый префикс входной переменной. В [5] показано, что при расширении a2 начального означивания a1 входной переменной вычисление для a2 включает вычисление для a1. При этом возможны следующие случаи.
1. Оно либо завершается с тем же результатом, что и при вычислении с означиванием a1. Это происходит в случае, когда вычисление с начальным означиванием a1 завершилось.
2. Оно может завершиться, хотя вычисление с начальным означиванием a1 не завершилось.
3. Оно может не завершиться, при этом вычисление с означиванием a1 также не завершается.
Действительно, увеличение длины означиваемого префикса входной переменной программы приводит к исключению ряда конъюнктов из ОДНФ, построенной по формуле, определяемой регулярным выражением.
Пример 1. Рассмотрим означивания префикса длины n > 0 входной переменной x = x0x1x2x3 … xi … в формуле 0(a0) (E(a0, x)E(a0, Out) ∨ ∪j=1,w (∩ h=0,j-1`Е(ah, x) S(ah, ah+1)) E(aj, x) Е(x, Out)).
Нетривиальным значением эта формула обладает, когда формула 0(a0) истинная, т.е. значение метапеременной a0 нулевое.
Базис индукции. При n = 1 возможны только два случая x0 = 0/ x0 = 1. При x0 = 0 формула E(a0, x) = ∩i=1,w`xi. Выходная метапеременная Out в этом случае нулевая. В оставшейся бесконечной дизъюнкции каждый конъюнктивный член содержит выражение Е(aj, x), j = 1, 2, … . Каждый такой член ложный в том случае, когда j – нечетно. Следовательно, бесконечная дизъюнкция эквивалентно преобразуется в бесконечную дизъюнкцию, в которые входят выражения E(aj, x), где j – четно. Выражение aj представляет число j. Следовательно, результирующая бесконечная дизъюнкция представляет предикат «число x – четно», и эквивалентно преобразуется в `x0. Случай, когда x0 = 1, эквивалентно преобразует исходное выражение в формулу, представляющую предикат «число x – нечетно», представляемый формулой x0. Итак, начальные означивания x0 = 0 / x0 = 1 порождают две формулы: `x0 и x0.
Индукционные рассуждения. Если n > 0, то, рассуждая как в предыдущем случае, можно показать, что при означивании sx = s0s1…sn-1 префикса переменной x исходное выражение эквивалентно преобразуется в формулу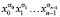 
, представляющую предикат «число x имеет своим префиксом sx». Таким образом, все эти наборы образуют 2n классов эквивалентности.
Пример 2. Рассмотрим программу, вычисляющую функцию x + y, в которой u, v суть рабочие переменные, причем u – выходная. Первая вершина есть функция присваивания u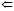 
x, следующий за ней цикл осуществляет прибавление к переменной u еще y единиц. Таким образом, на выходе программы формируется сумма x + y. Регулярное выражение, порождаемое этой программой, таково: 0(v) E(u, x) (`E(v, y) s(v) s(u))* E(v, y). Нетрудно убедиться, что для него справедливы приведенные выше рассуждения.
Классы неполных означиваний входной переменной программы
В этом разделе введем классификацию означиваний префиксов входной переменной программы. Справедлива следующая теорема.
Теорема 2. Пусть F(x) есть формула, представляющая функцию, вычисляемую программой p(x), и означивания a1 и a2 префиксов входной переменной находятся в отношении a1 < a2. Тогда справедлива импликация F(a2) ⊃ F(a1).
Следствие. Пусть ℑ1 есть множество вычислений, которые определяются программой p(a1) и ℑ2 – множество вычислений, которые определяются программой p(a2). Тогда справедливо включение ℑ2 ⊆ ℑ1.
Таким образом, программа p(a1) вычисляет функцию, которая является обобщением функции, вычисляемой программой p(a2).
Говорим, что логические формулы A и B находятся в отношении A # B, если неверны обе импликации A ⊃ B и B ⊃ A.
Теорема 3. Пусть формула F(x) представляет функцию, вычисляемую программой p(x), и a1, a2 суть означивания префиксов входной переменной, причем формулы F(a1), F(a2) находятся в отношении F(a1) # F(a2). Тогда:
1) имеются размеченные пути t1 и t2, такие, что t1 принадлежит программе p(a1) и не принадлежит программе p(a2), а t2 – принадлежит программе p(a2) и не принадлежит p(a1);
2) имеются конъюнкты C1 и C2, такие, что C1 принадлежит ОДНФ формулы F(a1) и не принадлежит ОДНФ формулы F(a2), а C2 – принадлежит ОДНФ формулы F(a2) и не принадлежит ОДНФ формулы F (a1).
Доказательство. Упомянутые конъюнкты C1 и C2 различаются подформулами Es, в которых один аргумент есть не полностью означенная входная переменная программы, а второй – рабочая метапеременная. Эти же конъюнкты определяют различные размеченные пути t1 и t2.
О длине вычисления программ
В этом разделе покажем, что длина вычисления программы определяется ее свойствами образовывать различные вычисления при означивании префикса ее входной переменной. Введем такое определение.
Пусть sx′ есть означивание префикса входной переменной программы p(x). Тогда двоичное число sx называется окончательным продолжением означивания sx′, если sx′sx есть двоичное число. Два означенных префикса sx′ и sx″ входной переменной программы p называются разделимыми, если имеется окончательное продолжение sx такое, что вычисления p(sx′sx) и p(sx″sx) различные.
Теорема 4. Пусть sx′ и sx″ суть два разделимых означивания и формула F(x) получена по регулярному выражению Rp. Тогда выполняется отношение F(sx′) # F(sx″).
Доказательство. Пусть окончательные означивания sx′sx и sx″sx определяют разные вычисления программы, т.е. им соответствуют разные размеченные пути. Тогда этим путям в ОДНФ формул F(sx′) и F(sx″) соответствуют две разные конъюнкции, которые истинны при различных означиваниях sx′sx и sx″sx входной переменной и при соответствующих правильных означиваниях метапеременных.
Следствие. Пусть формула F(x) получена по регулярному выражению Rp, и {sx′, sx″, …, sx(m)} попарно разделимые означивания префикса входной переменной программы. Тогда формулы F(sx′), F(sx″), …, F(sx(m)) попарно находятся в отношении #.
Справедлива теорема.
Теорема 5. Пусть {sx′, sx″, …, sx(m)} попарно разделимые означивания префикса входной переменной программы p(x). Тогда при всяком окончательном продолжении sx средняя длина вычислений p(sx(i) sx) не меньше log2 m, i = 1, 2, …, m.
Доказательство. Пусть формула F(x) представляет функцию, вычисляемую программой p(x). Каждое означивание sx(i) определяет совокупность конъюнктов в ОДНФ формулы F(sx(i)), которые содержат в качестве переменных не означенный суффикс входной переменной программы. При окончательном продолжении sx в точности один из них становится тождественно истинным и определяет значение программы p(sx(i) sx). Из соответствия конъюнктов ОДНФ формул F(sx(i)) и размеченных путей следует, что при окончательном продолжении sx существуют не менее m размеченных путей соответственно t1, t2, …, tm, начинающихся во входной вершине программы и оканчивающихся в заключительной. В совокупности они определяют однокорневое бинарное дерево T(sx) вычислений, в котором будет не менее m бинарных узлов, разделяющих эти размеченные пути t1, t2, …, tm. Поэтому средняя длина всех путей в нем не менее log2 m.
Следствие. Пусть {sx′, sx″, …, sx(m)} попарно разделимые означивания префикса входной переменной программы p(x). Тогда для всякого окончательного продолжения sx длина некоторого вычисления программы p(sx(i) sx) не меньше m, i = 1, 2, …, m.
Доказательство. Для получения 1 в l-м разряде, начиная с 0, оператору x + 1 требуется не менее 2l применений. В каждой совокупности конъюнктов, выделяемых означиваниями sx′, sx″, …, sx(m), имеется по меньшей мере одна подформула, которая имеет вид Es(sx(i)x′, a), где x′ – не означенный суффикс входной переменной программы и a – рабочая метапеременная, означенный префикс которой совпадает с sx(i).
Заключение
Приведена нижняя оценка вычислений арифметических программ в зависимости от предметной области, над которой вычисление осуществляется. Свойства предметной области описываются как совокупность попарно разделимых означиваний префикса входных переменных программ. При такой характеристике найдется вычисление, длина которого не меньше, чем мощность множества попарно разделимых означиваний префикса входа программы.
Библиографическая ссылка
Попов С.В. ИССЛЕДОВАНИЕ АРИФМЕТИЧЕСКИХ ПРОГРАММ // Научное обозрение. Технические науки. – 2019. – № 4. – С. 17-21;URL: https://science-engineering.ru/ru/article/view?id=1251 (дата обращения: 21.11.2024).