science-review.ru
В настоящей статье мы рассмотрим вопросы моделирования траекторий между преследующим и преследуемым объектами. На плоскости (или на поверхности) передвигаются два объекта, так как мы интерпретируем нашу задачу в задачу преследования, это участники задачи преследования. Объекты, преследующий и преследуемый, будут двигаться по определенной траектории преследования. Моделируемая траектория должна удовлетворять некоторым условиям. Одно из условий – это то, что минимальный радиус кривизны траектории не должен быть меньше некоторого порогового значения. Еще одно условие в рассматриваемой задаче – это то, что моделируемая траектория выходит под определенным углом из точки нахождения преследующего объекта и приходит в точку нахождения преследуемого объекта также под заданным углом. Будем рассматривать моделирование траектории в каждый момент времени, что предполагает точность вычислений. Теоретические положения для данной работы изложены в источниках [1, 2]. Некоторые особенности моделирования составных кривых взяты из источника [3].
Цель исследования: моделирование оптимальной траектории движения в каждый момент времени, при наличии ограничений на кривизну. Также, при заданных углах выхода преследующего объекта из точки нахождения и прихода в конечную точку преследуемого объекта под заданным углом. И описание нового алгоритма планирования заданной траектории в виде програм- много кода для применения нашего решения на практических задачах в областях робототехники, авиамоделирования, моделирования робототехнических комплексов и других моделях, где присутствуют элементы задачи преследования.
Материалы и методы исследования
Рассмотрим случай на горизонтальной плоскости проекций. Пусть преследуемый объект движется по траектории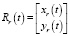 
, а преследующий объект движется по траектории 
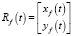(рис. 1).
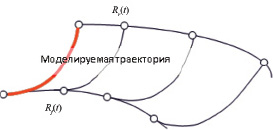
Рис. 1. Моделируемая траектория
В нашей задаче, которая решается в настоящей статье, моделирование траектории в каждый момент времени t. Моделируемая траектория может выходить из точки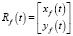 
под любым углом. Но в программном коде, написанном по материалам статьи, мы приняли угол между касательной к моделируемой траектории и касательной к траектории 
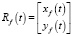равным 0, что не имеет принципиального значения в плане моделирования алгоритма. Также угол между касательной к моделируемой траектории и касательной к траектории 
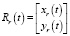в листинге программы принят равным 
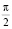. При этом моделируемая траектория имеет ограничения по своей кривизне. То есть радиус кривизны моделируемой кривой не может быть меньше некоторой пороговой величины. Реализация тестовых программ будет сделана в системе компьютерной математики MathCAD. Поскольку мы имеем дело с динамическими объектами, результат будет снабжен ссылкой на анимированные изображения.
При моделировании траекторий в задачах преследования, приняты во внимание работы, посвященные динамическим играм преследования [4], групповому преследованию [5], простому преследованию [6], расчету длин траекторий в задачах преследования [7].
Также использовались результаты, достигнутые в работе по играм преследования с интегрально-геометрическими ограничениями на функции управления преследователя [8].
Как возможность применения результатов, полученных в данной статье, рассматривалась работа моделирования задачи преследования в нейронных сетях [9].
Также приняты во внимание при написании статьи методы коллективного преследования, изложенных в работах [10, 11].
Результаты исследования и их обсуждение
Моделирование окружности у преследующего объекта
Мы уже говорили, что преследующий объект движется по траектории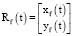 
(при моделировании общего алгоритма угол между траекторией и ее касательной не имеет принципиального значения). Выполнение условия того, что угол между касательными к моделируемой траектории и к траектории 
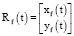равен 0, и условие ограничения по кривизне, приводят к построению окружности, изображенной на рис. 2.
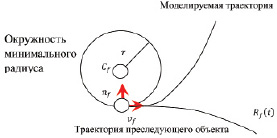
Рис. 2. Окружность к траектории преследующего объекта
На рис. 2 показано, что вдоль траектории преследующего объекта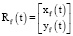 
формируется локальный динамический базис (vf, nf), где vf – единичный вектор, сонаправленный с вектором скорости 
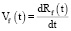преследующего объекта. Вектор nf – есть вектор нормали к касательной к траектории 
.
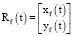Отсюда следует, центр моделируемой окружности Cf(t) формируется следующим образом: Cf(t) = Rf(t) + r?nf(t), где r – это минимальный пороговый радиус траектории преследующего объекта.
Центр окружности может формироваться иначе (рис. 3):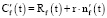 
. В таком случае (как на рис. 3) моделируемая траектория выходит под углом ∞ к траектории преследующего объекта 
.
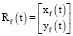В коде программы, написанной по материалам статьи, угол между траекториями равен 0.
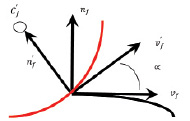
Рис. 3. Формирование окружности на траектории преследующего объекта
Моделирование окружности у преследуемого объекта
Рассмотрим формирование окружности при входе моделируемой траектории в траекторию преследуемого объекта (рис. 4). Здесь центр окружности формируется так: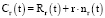 
, где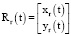 
– это точка траектории преследуемого объекта, а r – минимальное значение радиуса моделируемой траектории. Здесь направление вектора nr(t) полностью определяется направлением вектора Vm(t) скорости моделируемой траектории в момент пересечения с траекторией преследуемого объекта 
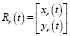. Векторы nr(t) и Vm(t) должны быть перпендикулярны. В листинге программы по материалам статьи используется перпендикулярность векторов Vm(t) и vr.
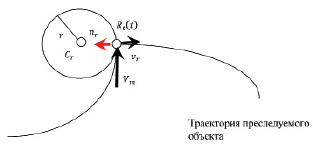
Рис. 4. Моделирование окружности у преследуемого объекта
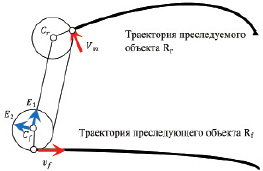
Рис. 5. Линия сопряжения в моделируемой траектории
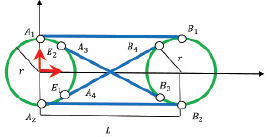
Рис. 6. Сопряжение двух окружностей
Линии сопряжения между двумя окружностями
Рассмотрим вопрос о сопряжении между двумя окружностями одного радиуса передвигающимися по траекториям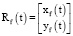 
и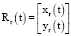 
(рис. 5).
Исходя из данных, представленных на рис. 5, к построению общей касательной между окружностями (Cf, r) и (Cr, r). Если мы перейдем в систему координат, образованную точкой Cf(t) и векторами (рис. 6):
, 
,
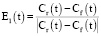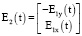то задача построения линий сопряжения между двумя окружностями преобразуется к виду, изображенному на рис. 6, где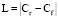 
. Как видно на рис. 6, существует четыре варианта линии сопряжения. Выбор варианта сопряжения оставим разработчику. Кроме того, существуют варианты расположения окружностей, которые изображены на рис. 7. В листинге программы, написанной по материалам статьи, мы использовали один вариант взаимного расположения окружностей и построили для демонстрации четыре линии сопряжения.
Для точек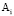 
, 
, 
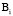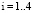на рис. 6 существуют решения:
, 
,
,
,
, 
,
,
.
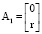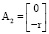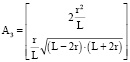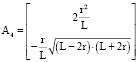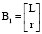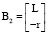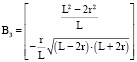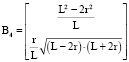Но эти решения найдены для локальной системы координат (Cf, E1, E1) (рис. 5), чтобы перевести точку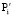 
, принадлежащую отрезку 
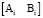, в мировую систему координат (О, Н1, Н2), необходимо выполнить преобразование по формуле
,
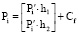где h1, h2 – это векторы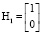 
и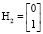 
, разложенные по векторам базиса (Cf, E1, E1), то есть путем преобразования уже в мировую систему координат 
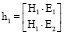и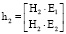 
.
Заключение
Результаты моделирования траекторий
В настоящей статье предлагаются модели и алгоритмы моделирования траектории путем решения задачи преследования. По результатам, изложенным в данной статье, был написан программный код в системе компьютерной математики MathCAD. С текстом программы можно ознакомиться на следующем ресурсе [12]. Кроме того, по результатам работы программ изготовлено анимированное изображение, которое можно просмотреть в следующем источнике [13].
В процессе выполнения программы моделируемая траектория перейдет на прямую линию, если в момент отрыва от траектории преследующего объекта совершит движение по часовой стрелке, то есть в обратном направлении. Для перехода на прямолинейный отрезок, точка после отрыва от траектории преследуемого объекта должна совершить путь равный почти полной окружности по направлению против часовой стрелки. Далее мы видим, что точка моделируемой траектории сходит с траектории преследующего объекта по часовой стрелке и входит в траекторию преследуемого объекта под прямым углом (частный случай нашей постановки задачи, так как в начале при постановке задачи мы задали угол вхождения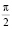 
), но уже по направлению часовой стрелки. Точка моделируемой траектории отрывается от траектории преследующего объекта и переходит на прямолинейный участок (траектория данной точки в этот момент времени становится прямой линией) и входит в траекторию преследуемого по часовой стрелке.
Предполагается, что данные модели и алгоритм решения поставленной задачи являются актуальными так как результаты работы могут быть использованы при решении прикладных задач робототехники, авиамоделирования, моделирования робототехнических комплексов и других моделей, где присутствуют элементы задачи преследования.
Библиографическая ссылка
Нефедова В.А., Дубанов А.А. МОДЕЛИРОВАНИЕ ТРАЕКТОРИИ С ОГРАНИЧЕНИЯМИ НА КРИВИЗНУ // Научное обозрение. Технические науки. – 2019. – № 6. – С. 38-43;URL: https://science-engineering.ru/ru/article/view?id=1268 (дата обращения: 24.04.2024).