Еще с давних времен у человечества возникла потребность в случайных числах из-за большей популярности выборочного наблюдения вместо сплошного. Во времена появления первых ЭВМ появился огромный интерес к проблеме, заключавшейся в получении случайного числа, потому что ЭВМ дает новые возможности для работы со случайными числами. Широко распространенные генераторы случайных чисел основаны на компьютерных алгоритмах и математических преобразованиях, либо на цифровых, аналоговых схемах или особых аппаратных средствах, реагирующих на различным параметры окружающей среды, которые имеют случайный характер поведения. Несмотря на сложность различных физических законов и математических формул, на которых основывается принцип работы генератора, их последовательность чисел является псевдослучайной, так как теоретически существует возможность их восстановить [1].
Цель исследования: определить сущность случайности квантовых генераторов, рассмотреть категории генераторов и выявить их преимущества и недостатки.
Материалы и методы исследования
Считается что для генерации наиболее случайного числа необходимо использовать аппаратный генератор – устройство, генерирующее случайную последовательность чисел на основе вычисляемых, хаотически изменяющихся параметров происходящего физического процесса. Функционирование этих устройств чаще всего основывается на использовании таких надежных источников энтропии, как дробовой шум, фотоэлектрический эффект, тепловой шум, квантовые явления и т.д. Эти процессы считаются наиболее непредсказуемыми. Полученная последовательность случайных чисел возникает в результате измерения состояния физической системы, которая бывает на основе классической и квантовой физики. Если генератор основывается на законах классической физики, то случайность зависит только от неопределенности начальных условий [2]. Таким образом, начальные условия, на основе даже сложного закона классической эволюции, могут быть восстановлены, следовательно, и взломан генератор случайной последовательности. Теоретически генераторы на основе классической физики являются псевдослучайными генераторами, но на практике в настоящее время еще не придумано способа нахождения начальных условий для сложных явлений, поэтому на данный момент они также считаются случайными.
Однако с учетом скорости развития технологий и человечества в целом, не так много осталось времени до нахождения ответов для сложных явлений в классической физике. Поэтому нужно заранее быть готовым к массовым хакерским атакам на подобные системы. Для предотвращения таких взломов необходимы истинно случайные генераторы. По-настоящему случайную последовательность можно получить из явлений, принадлежащих квантовой физике. Так, результаты работы квантового генератора, находящегося каждый раз в одинаковом состоянии, имеют абсолютно случайный характер. В квантовой механике система может быть получена в суперпозиции базисных состояний (измерений), как показано на рис. 1.
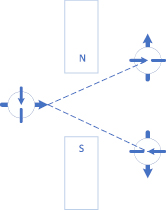
Рис. 1. Суперпозиции базисных состояний
У полностью способного квантового компьютера хватит мощности, чтобы декодировать вычисления, которые создают любую текущую форму шифрования. Например, квантовый компьютер с 300 квантовыми кубитами может проводить больше вычислений, чем атомов во Вселенной.
Квантовые генераторы случайных чисел (Quantum random number generator – QRNG) можно разделить на три основные категории, основываясь на уровне надежности устройств:
– практический (доверенный) QRNG – способен генерировать случайность на высоких скоростях, так как построен на оттестированных и откалиброванных устройствах;
– самотестируемый QRNG – умеет генерировать случайную последовательность без доверия к реализации устройств;
– полусамотестируемый QRNG – является чем-то средним между практическим и самотестируемым генератором, обеспечивая компромисс между скоростью генерации случайных чисел и надежностью устройства.
Практический QRNG обычно разрабатывают с использованием несложного процесса, как показано на рис. 1. Существует огромное количество практических генераторов случайных последовательностей на основе различных реализаций приведенного процесса. Как правило, такие генераторы имеют низкую стоимость аппаратной реализации и высокую скорость генерации случайной последовательности.
Из любого квантового процесса, нарушающего когерентную суперпозицию состояний, может быть порождена истинная случайность. Большая часть современных практических QRNG реализованы в фотонных системах, это связано с потенциальной возможностью интеграции чипов по размерам и наличием высококачественных оптических компонентов [3].
Случайные биты могут быть получены естественным путем: путем измерения кубита. Кубит – это двухуровневая квантово-механическая система, которая, подобно биту в классической теории информации, является фундаментальной единицей квантовой информации.
Один из вариантов увеличения скорости генерации случайной последовательности – это проведение измерений временного или пространственного режима фотона, относящиеся к многомерному квантовому пространству.
Временные QRNG измеряют время прихода фотона. Одним из важных преимуществ данного QRNG является то, что из однофотонного детектирования может быть извлечено более одного бита случайного числа, что улучшает скорость генерации случайных чисел. Период времени обычно устанавливается равным времени простоя детектора. По сравнению с кубитом QRNG, временной режим QRNG уменьшает влияние мертвого времени обнаружения.
Подобно случаю временного QRNG, несколько случайных битов могут быть сгенерированы путем измерения пространственного режима фотона с помощью системы обнаружения с пространственным разрешением. Одним из наглядных примеров является передача фотона через светоделитель 1×N и определение положения выходного фотона. Пространственный QRNG предлагает такие же свойства, как и временной QRNG, но он требует нескольких детекторов. Кроме того, корреляция может быть введена между случайными битами из-за перекрестных помех между различными пикселями в плотно упакованном массиве детекторов.
Случайность в практических QRNG в большинстве случаев достаточна для реальных задач, при условии правильной реализации модели. Однако такие генераторы теряют свою безопасность в случае, если устройство управляется противником. Например, в случаях, когда QRNG полностью поставляется производителем с плохим умыслом. Такой производитель способен копировать очень длинную случайную последовательность на большой жесткий диск и только выводить номера с жесткого диска в последовательности, производитель всегда может узнать результат работы устройства QRNG.
Также возможна реализация QRNG, у которого выходная случайная последовательность не будет иметь зависимость от физических реализаций. Истинная случайность может быть сгенерирована путем самотестирования даже на не совсем идеальной реализации генератора.
Суть самотестирования QRNG основана на независимом от устройства рассмотрении квантовой запутанности или нелокальности путем наблюдения за нарушением неравенства Белла [4] (рис. 2). Джон Стюарт Белл (28 июня 1928 – 1 октября 1990) является физико-теоретиком, который сформулировал и доказал неравенства Белла (теорему Белла), впоследствии заложил теоретическую основу для экспериментальных исследований ЭПР-парадокса.
Преимуществом этого типа QRNG является свойство самотестирования случайности. Даже если выходная случайность смешивается с нехарактерным классическим шумом, все равно существует возможность получить некоторую часть подлинной случайности, основанную на количестве наблюдаемой нелокальности. Скорость генерации самотестирующегося QRNG является очень низкой, так как такой генератор должен демонстрировать нелокальность. Исходя из этого, для тестов Белла требуется использовать случайные входные данные, начинающиеся с короткого случайного числа. Поэтому такой процесс генерации случайности также называется расширением случайности [5].
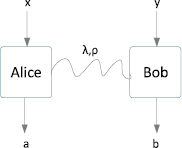
Рис. 2. Иллюстрация двудольного теста Белла
Для случайных входов x и y две пространственно-разделенные стороны Alice и Bob выводят значения a и b соответственно, без сигнализации. Неравенство Белла определяется как линейная комбинация вероятностей p(a, b|x, y).
В построенных на абсолютно случайных входах самотестируемых генераторах, выходной поток случайности содержит нарушения тестов Белла, и обратно: когда множество входных данных предопределено, всякое неравенство Белла может быть отклонено до допустимой произвольной величины, исключая вызов квантового параметра. Все протоколы самотестирующих генераторов данные условия не поддерживают. Кроме того, сохраняется актуальная проблема – генерация случайности при наличии частичной случайности, ведь нарушитель может использовать дополнительные сведения о входах для подделки отклонений неравенств Белла. Усиление случайности, когда от любой частичной случайности генерируется свободная произвольная случайность, невозможно получить в стандартных процессах.
Обычно генератор состоит из системы считывания и источника случайности. В современных алгоритмах некоторая часть реализована достаточно хорошо, а другая – нет. Данный факт подвигает к созданию промежуточного типа генераторов случайной последовательности. Такой генератор называется полусамотестируемым. В соответствии с несколькими гипотезами, случайность может генерироваться без полной характеристики устройств, к примеру, надежная случайность может быть сгенерирована с помощью достоверной системы считывания и различного недостоверного объекта случайности. Компромисс между самотестирующимся и практическим генераторами, которым соответственно характерны достаточная безопасность сертифицированной случайности и высокая производительность с низкой стоимостью, обеспечивает полусамотестирующийся генератор случайной последовательности [6].
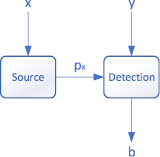
Рис. 3. Полусамотестирующийся генератор случайной последовательности
Проанализировав рис. 3, можно удостовериться, что стандартный генератор состоит из двух основных модулей, а именно источника генератора и измерительного устройства. Источник генератора распространяет квантовые состояния, а измерительный прибор отслеживает эти состояния и выпускает случайные биты. В надежном устройстве стандартного генератора случайной последовательности источник и измерительные устройства должны быть спроектированы достаточно хорошо. В самотестируемом генераторе случайность выхода не связана с устройствами реализации. На иллюстрации полуавтоматического тестирования QRNG, независимая от источника схема представлена уникальным x, соответствующим состоянию ρx, и несколькими вариантами настроек измерения y [7].
За последние два десятилетия произошла огромная разработка для всех трех типов квантовых генераторов случайных чисел.
Результаты исследования и их обсуждение
Из всякого квантового процесса, нарушающего когерентную суперпозицию состояний, может быть сгенерирована истинная случайность. Множество практических генераторов спроектированы в фотонных системах по причине присутствия высококачественных оптических свойств и потенциала интеграции с размером чипа. Стандартный генератор содержит источник энтропии, который генерирует четкие определенные квантовые состояния, и надлежащую систему обнаружения. Обычно на выходе личная квантовая случайность слита с классическими шумами. В совершенстве, извлекаемая квантовая случайность должна быть достаточна предопределена количественно и должна быть главным источником случайности. Настоящая случайность может быть извлечена из состава квантового и классического шума.
Случайность имеет решающее значение практически для всего, что мы делаем с нашей вычислительной и коммуникационной инфраструктурой. В частности, она используется для шифрования данных, защищая все: от мирных разговоров до финансовых транзакций и государственных секретов [8].
Подлинную, поддающуюся проверке случайность, чрезвычайно трудно найти. Но это может измениться, как только квантовые компьютеры продемонстрируют свое превосходство. Случайность и квантовая теория идут вместе. В обоих случаях первое является неизбежным следствием второго [9].
Законы квантовой механики не диктуют определенный результат измерения – только вероятности каждого результата. Это делает его идеальным источником случайных чисел. Системы с непрерывными переменными имеют высокую пропускную способность и эффективные детекторы по сравнению с их дискретными переменными аналогами. Кроме того, квантовые генераторы случайных чисел имеют преимущество перед обычными источниками случайности в том, что они неуязвимы для воздействий окружающей среды и позволяют проводить проверку статуса в реальном времени [10].
Заключение
Основными категориями квантовых генераторов случайности являются практический, самотестируемый и полусамотестируемый QRNG. Преимуществом первого считаются высокая производительность и низкая стоимость, а недостатком – безопасность. Самотестируемый генератор не обладает достаточной скоростью, как практический, но имеет высокую безопасность сертифицированной случайности. Полусамотестируемый генератор является компромиссным решением между практическим и самотестируемым генераторами.
Библиографическая ссылка
Горбачев А.А., Кухтинов В.Н., Черкесова Л.В. СЛУЧАЙНОСТЬ КВАНТОВЫХ ГЕНЕРАТОРОВ // Научное обозрение. Технические науки. 2020. № 2. С. 27-31;URL: https://science-engineering.ru/ru/article/view?id=1283 (дата обращения: 03.03.2026).


 science-review.ru
science-review.ru