science-review.ru
В решении задач простого преследования на плоскости с использованием стратегии параллельного сближения используются окружности Аполлония.
Окружность Аполлония – геометрическое место точек плоскости, отношение расстояний от этих точек до двух других заданных точек, величина постоянная k = Const и k ≠ 0.
Рассмотрим данную окружность на примере старинной задачи о флибустьерах.
Задача состоит в том, что флибустьеры с острова Ямайка узнали, что на якоре перед Пуэрто-Бельо стоит испанский галеон, забитый до верха золотом. И как только непогода отступит, галеон выйдет в Карибское море и возьмет курс на пролив между островам Гаити и Пуэрто-Рико. Флибустьеры также ждут хорошей погоды, поэтому выйти из Кингстона они могут только одновременно с испанским галеоном. Вопрос такой, что флибустьерам нужно выбрать такой курс, который наверняка поможет им успеть перехватить испанцев. Если флибустьеры точно знают, во сколько раз скорость их корабля больше скорости галеона, то они могут найти все точки, в которые их корабль и испанский галеон могут попасть одновременно. Пусть отношение скоростей судов равно k > 1, так как корабль пытается догнать другое судно, и отношение их расстояний, пройденных до момента встречи, также равно k. Следовательно, все возможные точки встречи лежат на ГМТ (геометрическое множество точек) К таких, что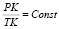 
, где точки P и T соответствуют Пуэрто-Бельо и Кингстону. Таким ГМТ является окружность, которую называют окружностью Аполлония.
Далее будем рассматривать общий случай этой задачи.
Простым движением точки называется движение, когда пройденное расстояние S есть линейная функция времени: S(t) = v·t, где v = Const – модуль скорости точки.
Из вышесказанного следует, что окружность Аполлония – это геометрическое место точек, когда |KP| / (|KT| = Const) (рис. 1).
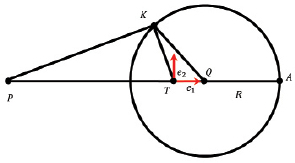
Рис. 1. Окружность Аполлония
Применительно к задачам преследования окружность Аполлония имеет следующий смысл. Если преследователь и цель в определенный момент времени имеют положения на плоскости P и T, и значения скоростей, равные по модулю VP и VT соответственно.
Тогда ГМТ точек K, как место возможных встреч преследователя P с целью T, есть окружность радиуса |QK| с центром в точке Q [1, 2].
Направления скоростей преследователя и цели являются взаимосвязанными. То есть направление скорости цели диктует направление скорости преследователя или, наоборот, направление преследователя определяет направление цели, чтобы обеспечить встречу в точках, принадлежащих окружности Аполлония.
Целью данной статьи является формализация и алгоритмизация метода параллельного сближения преследователя и цели.
Расчет параметров окружности Аполлония
То, что данное множество точек K является окружностью, было известно еще древним математикам, но мы приведем выкладки расчета окружности и ее центра.
Введем ортонормированную систему координат (e1, e2) с центром в точке T (рис. 1), вектор e1 сонаправлен вектору PT. Пусть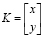 
, а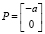 
, где a = |PT|. Тогд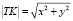а 
, а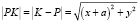 
. Из условия того, что преследователь и преследуемый приходят в точку K одновременно, имеем следующее: 
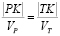. Следовательно, 
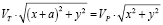. После возведения в квадрат и раскрытия скобок получаем уравнение
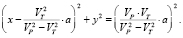
Полученное уравнение в системе (e1, e2) с центром в точке T описывает окружность радиуса R и с центром в точке Q:
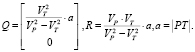
Отметим одну характеристическую точку, называемую точкой Аполлония:
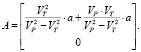
Моделирование итерационного процесса задачи преследования
Факт того, что стратегия преследователя в задаче преследования с помощью метода параллельного сближения является оптимальной в плане максимального сокращения времени поимки цели преследователя, доказан в работах Л.О. Петросяна [1–3]. Также вопросы оптимального сближения рассматривались в работах одного из основоположников теории дифференциальных игр [4].
Будем считать, что для нашего итерационного процесса известны начальные данные P0 и T0. Скорости преследующего и преследуемого объектов постоянны и равны по модулю VP и VT соответственно. Траектория преследуемого объекта в нашей модели является предопределенной, поэтому мы сможем рассчитать массив точек {Ti}, где дистанция между точками Ti и Ti+1 равна
|Ti+1 – Ti| = VT·T,
T – период дискретизации по времени.
Итерационная схема расчета координат преследователя, координат центров окружностей Аполлония, радиусов окружностей Аполлония, характеристических точек представлена на рис. 2.
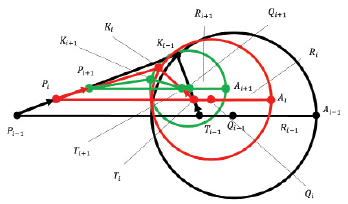
Рис. 2. Итерационная схема
Координаты преследователя на i-м шаге итераций будут такие:
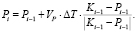
Радиус окружности Аполлония будет таким:
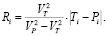
Центр окружности Аполлония рассчитывается так:
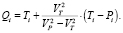
Координаты точки Ki есть продукт решения системы уравнений относительно непрерывного параметра t:
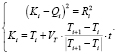
Разрешенная относительно параметра t вышеуказанная система представляет собой корни квадратного уравнения, вывод которых в данной статье мы приводить не будем из-за громоздких выражений.
В тестовой программе, написанной по материалам статьи, решение квадратного уравнения написано в виде отдельной процедуры – функции. С текстом тестовой программы можно ознакомиться в [5].
То, что отрезок [Pi, Ti] останется параллельным отрезку [P0, T0], не вызывает сомнений. Рассмотрим первый отрезок [P1, T1]. Координаты точек P1 и T1 равны (рис. 3):
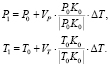
Исходя из того, что преследователь и его цель должны прийти в точку K на окружности Аполлония одновременно, мы вправе сделать вывод, что
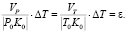
Далее:
Другими словами, вектор P1T1 сонаправлен вектору P0T0 и перпендикулярен вектору нормали N (рис. 3).
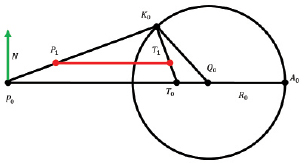
Рис. 3. Параллельное сближение преследователя и цели
Результаты моделирования задачи преследования методом параллельного сближения
Нами была написана тестовая программа, скриншот результатов работы которой показан на рис. 4. На рисунке видно, что отрезки [Pi, Ti] образуют однопараметрическую последовательность параллельных [P0, T0] линий.
Также на рис. 4 показано, что точки Pi, Ti, Qi, Ai принадлежат одной прямой. Показан подвижный треугольник Pi, Qi, Ki, который сходится к точке встречи преследователя и цели.
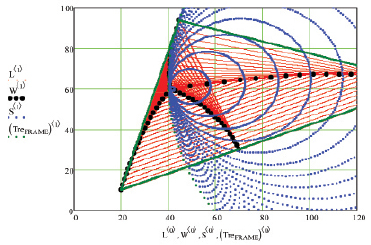
Рис. 4. Перехват цели
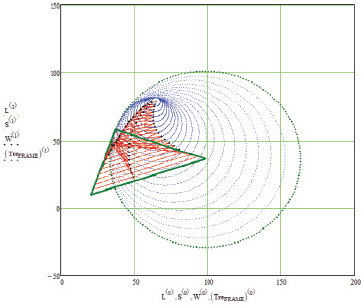
Рис. 5. Моделирование убегания цели от преследователя
Глядя на рис. 4, а именно на однопараметрическое множество окружностей Аполлония, сходящееся к точке встречи, может возникнуть обманчивое впечатление, что все множество окружностей касается в точке встречи преследователя и цели. В следующей модели с иной траекторией цели мы покажем, что это не так.
Рис. 4 дополнен ссылкой на анимированное изображение [6], где можно просмотреть, как изменяется во времени расположение преследователя, цели, точек на окружности Аполлония.
Итак, ситуацию, представленную на рис. 4, можно интерпретировать как моделирование перехвата преследователем цели.
Ситуацию, представленную на рис. 5, можно интерпретировать как моделирование процесса ухода преследуемого объекта от преследователя [7].
На рис. 5 также показан подвижный треугольник Pi, Qi, Ki, точки Pi, Ti, Qi, Ai и окружности Аполлония. Хотелось бы обратить ваше внимание на поведение точки Ki, оно похоже на поведение точки возврата второго рода. Здесь как раз наблюдается схождение окружностей Аполлония к точке встречи преследователя и цели, но множество окружностей не является касательными в одной точке [7].
Обсуждение полученных результатов
По материалам, изложенным в данной статье, были написаны тестовые программы в системе компьютерной математики MathCAD 15. Тексты программ выложены на ресурсе одного из авторов [5]. Ссылки на анимированное изображение изготовленных по результатам работы программ доступны на ресурсах [6, 7]. При написании данной статьи были приняты во внимание достижения, изложенные в работах [8–10]. Также использованы результаты, изложенные в работах [11–13].
Заключение
Целью данной статьи было показать движение всех характеристических линий и точек в реализации метода параллельного сближения в задачах простого преследования на плоскости. Была достигнута формализация и алгоритмизация метода параллельного сближения преследователя и цели.
Показано движение окружности Аполлония, ее схождение к точке (месту) встречи преследователя и цели. Показано, как сходится отрезок, соединяющий преследователя и цель, будучи параллелен самому себе. Показано, как направления скоростей преследователя и цели являются взаимосвязанными. То есть направление скорости цели диктует направление скорости преследователя или, наоборот, направление преследователя определяет направление цели, чтобы обеспечить встречу в точках, принадлежащих окружности Аполлония.
При геометрическом моделировании методом параллельного сближения необязательно вычислять параметры окружности Аполлония. Достаточно будет строить однопараметрическое множество параллельных линий, соединяющих преследователя и преследуемого, окружность, с радиусом равным шагу преследователя, чтобы найти точку следующего положения преследователя.
Библиографическая ссылка
Нефедова В.А., Дубанов А.А. ВИЗУАЛИЗАЦИЯ ОКРУЖНОСТЕЙ АПОЛЛОНИЯ ПРИ ГЕОМЕТРИЧЕСКОМ МОДЕЛИРОВАНИИ МЕТОДА ПАРАЛЛЕЛЬНОГО СБЛИЖЕНИЯ НА ПЛОСКОСТИ // Научное обозрение. Технические науки. – 2020. – № 4. – С. 70-75;URL: https://science-engineering.ru/ru/article/view?id=1306 (дата обращения: 26.04.2024).