Псевдослучайные числа (ПСЧ) – значения, которые возникают при помощи некоторого закона распределения. Если на мгновение задуматься, то закон распределения – это некоторая математическая функция, которая формирует значение на основе некоторого первоначального числа. Возникает вопрос, откуда взять начальное значение?
На самом деле существует довольно много способов для определения первоначального числа, либо взять максимально возможный диапазон значений и выбрать случайное число, либо при помощи некоторого алгоритма сформировать значение и так далее.
Для конкретной статьи был выбран алгоритм формирования начального числа с помощью порядка точки эллиптической кривой.
На данный момент существует множество интерпретации в понимании, что такое эллиптическая кривая. На самом деле достаточно будет понимать, что это просто множество точек, описываемое следующим уравнением [1]:
y2 = x3 + ax + b. (1)
В первую очередь при работе с эллиптическими кривыми необходимо исключить особые кривые. То есть нужно прописать проверку, при которой неравенство (2) будет выполняться.
4a3 + 27b2 > 0. (2)
После проверки эллиптической кривой необходимо отметить, что у каждого ненулевого элемента так называемой точки есть либо два корня, либо нет ни одного. Поэтому точки кривой разбиваем на пары следующего вида:
P = (x, y) и 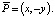 (3)
(3)
Важным фактором в эллиптических кривых является то, что любая прямая, проходящая через две различные точки, пересекает данную кривую в третьей точке. Кроме точек перегиба, касательная, проведенная к кривой, пересекает её еще в одной точке. Симметрия кривой относительно Ох позволяет дать наглядное определение обратной к рассматриваемой точке.
Введем две операции, которые можно выполнять над точками [2]:
1) сложение точек – результат суммирования двух точек эллиптической кривой, в конечном итоге которого появляется обратная третья точка;
2) умножение точки на число – прибавление рассматриваемой точки к самой себе K раз.
Разберемся еще с одним понятием, таким как порядок точки кривой – число, при умножении на которое возникает точка на бесконечности.
Так как в дальнейшем подразумевается работа с ПСЧ, необходимо обратить внимание на следующие свойства, которые позволяют определить точки эллиптической кривой над конечными полями:
1) некоторые значения y2 не имеют квадратного корня по модулю 13;
2) каждая точка имеет инверсию;
3) точки инверсии находятся на тех же самых вертикальных линиях.
После определения эллиптических кривых разберемся с понятием ПСЧ [3]. Важно отметить, что под случайной величиной стоит понимать некоторое значение, полученное в результате опыта. Причем появление той или иной величины нельзя предсказать совершенно точно до её измерения. Поэтому последовательность будет считаться случайной тогда и только тогда, когда следующий шаг никак не зависит от предыдущего.
Исходя из вышеописанного утверждения, формирование ПСЧ основывается на некотором алгоритме, который позволяет в результате получать значения, отличные друг от друга, и подчинен определенному заданному закону распределения.
На практике используются следующие способы генерации случайных чисел (ГСЧ):
- аппаратный, реализация которого не требует дополнительных вычислительных ресурсов ЭВМ по выработке случайных чисел, а необходима только операция обращения к внешнему устройству, так называемому датчику.
- табличный, реализация которого требует определенных затрат в памяти ЭВМ, так как полученные значения записываются в таблицу и хранятся на компьютере;
- алгоритмический, реализация которого при формировании случайных чисел требует больших затрат ресурсов ЭВМ с помощью специальных алгоритмов и реализующих программ.
Для достижения «идеального» ГСЧ необходимо придерживаться следующих правил:
- занимать минимальный объем машинной памяти и времени;
- иметь неповторяющиеся числа;
- быть воспроизводимым;
- содержать статистически независимые числа;
- состоять из квазиравномерно распределенных чисел.
Теперь, после краткого обзора про ПСЧ, разберемся с регистром сдвига с линейной обратной связью [4].
Данный регистр состоит из двух частей:
- регистр сдвига;
- функция обратной связи.
Пример регистра сдвига с линейной обратной связью (РСЛОС) представлен на рис. 1.
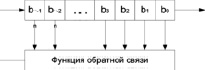
Рис. 1. Регистр сдвига с линейной обратной связью
Сам регистр сдвига представляет собой последовательность бит, число которых определяет длину регистра. При каждом извлечении бита все биты сдвигаются вправо на одну позицию в сторону младших разрядов.
В качестве обратной связи выступает любая математическая функция, которая производит действие над битами. В рамках статьи будет использоваться XOR-преобразование случайных бит. Запись в РСЛОС производится в виде полиномов. Важно отметить, что степень первого полинома указывает на количество битов в регистре сдвига, а степенные показатели остальных элементов полинома указывают, какие будут использованы ячейки регистра сдвига при съеме битов для математических операций.
Обобщая полученные утверждения, можно сказать, что n-битовый регистр сдвига с линейной обратной связью может находиться в одном из 2n – 1 внутренних состояний.
Рассмотренный регистр может генерировать ПСП с использованием эллиптических кривых над конечными полями.
Распишем пошагово алгоритм формирования ПСЧ:
- выбираем конечное поле;
- выбираем ЭК, в которой не будут присутствовать исключения;
- выбираем точку ЭК порядка K;
- выбираем примитивный многочлен для формирования регистра сдвига;
- вычисляем последовательность P с использованием M-последовательности q с выходом конечного элемента;
- преобразуем полученное значение в двоичную последовательность с использованием оператора отображения;
- после преобразуем целое число из двоичной последовательности [5].
Исходя из вышеописанного алгоритма, был разработан программный продукт, при помощи которого можно получить ПСЧ или ГСП с использованием порядка выбранной точки, принадлежащей ЭК. На блок-схеме, представленной на рис. 2–3, структурно показано тело программы.
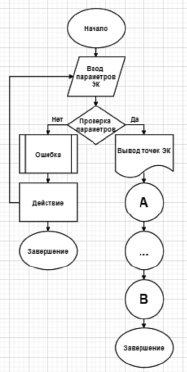
Рис. 2. Блок-схема программы (ч. 1)
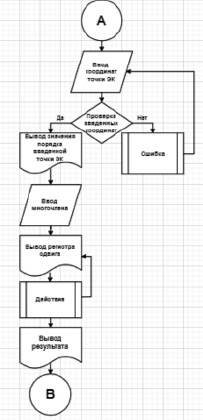
Рис. 3. Блок-схема программы (ч. 2)
Опишем более детально функционал программного средства.
Для удобства работы с программой был разработан интерфейс, представленный на рис. 4 [6].
На начальном этапе пользователю необходимо ввести параметры эллиптической кривой. В качестве проверки введем следующие параметры: E211 (5, -4). Данное действие продемонстрировано на рис. 5. Выбранное поле должно быть простым числом, а параметр «а» – взаимно простым с конечным полем.
Прежде чем продолжить работу с программой, нужно удостовериться в правильности введенных параметров. Для этого была разработана проверка, чтобы исключить возможность ошибочного ввода данных. Описанное действие выполняет специальная кнопка, представленная на рис. 6.
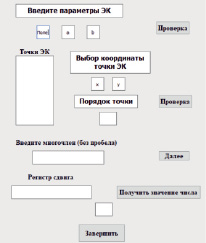
Рис. 4. Визуальное окно программы
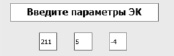
Рис. 5. Окно ввода данных

Рис. 6. Кнопка, отвечающая за проверку введенных данных
После проверки введенных параметров, если данные – корректны, то в том случае в окне, показанном на рис. 7, будет выведено множество точек, принадлежащих рассматриваемой эллиптической кривой.

Рис. 7. Окно вывода точек ЭК
Исходя из рис. 7, можно утверждать, что введенные пользователем параметры – корректны, следовательно, в окне ввода координат точки ЭК, представленной на рис. 8, выбирается точка, которая принадлежит множеству точек эллиптической кривой. В виде исключения была написана проверка ввода корректных данных пользователем. За описанное действие отвечает кнопка, показанная на рис. 9.
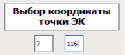
Рис. 8. Окно ввода координат точки ЭК

Рис. 9. Кнопка проверки корректности ввода данных
В том случае, если проверка успешно пройдена, определяется порядок выбранной точки, как видно из рис. 10.

Рис. 10. Окно вывода порядка точки ЭК
После вывода числа пользователю предоставляется возможность для ввода многочлена вида
xn + x(n – 1) +?+ x(n – (n – 1)) + 1,
где n – максимальная степень многочлена и длина регистра сдвига.
В качестве проверки на рис. 11 продемонстрирован многочлен.

Рис. 11. Окно ввода полинома
После нажатия на кнопку далее, как показано на рис. 12, при помощи преобразований получаем регистр сдвига. Окно вывода представлено на рис. 13.

Рис. 12. Кнопка для преобразования регистра сдвига
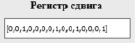
Рис. 13. Окно вывода сдвигового регистра
Затем, при нажатии на кнопку, показанную на рис. 14, формируется ПСЧ на основе полученного регистра сдвига, путем выбранной случайной последовательности бит регистра. Полученный результат отображается в окне вывода, представленном на рис. 15.

Рис. 14. Формирование ПСЧ

Рис. 15. Окно вывода результата
Если необходимо вывести сгенерированную последовательность без повторяющихся значений, а не одно, то необходимо нажимать на кнопку, показанную на рис. 14, до тех пор, пока не выведется окно вывода, которое продемонстрировано на рис. 16, и затем, нажав на кнопку, показанную на рис. 17, можно просмотреть сгенерированную последовательность, результат которой приведен на рис. 18. После окончания работы с программным средством необходимо нажать на кнопку, показанную на рис. 19.
Рис. 16. Окно вывода

Рис. 17. Кнопка, отвечающая за вывод генератора
Рис. 18. Фрагмент полученной последовательности

Рис. 19. Завершение работы программы
Теперь опишем функционал программного средства.
На рис. 20 можно наблюдать функцию, которая отвечает за проверку введенных пользователем параметров ЭК. Изначально проверяется на простоту. Затем, после прохождения условия, проверяется параметр а. Если рассматриваемый параметр имеет отрицательное значение, то к нему прибавляется значение поля, для исключения особых кривых. После необходимо, чтобы наибольший общий делитель поля, относительно параметра а, был равен 1.
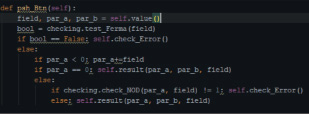
Рис. 20. Проверка введенных параметров ЭК
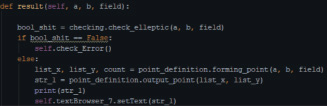
Рис. 21. Функция генерации точек ЭК
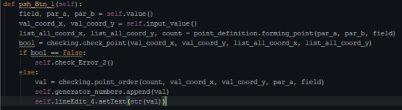
Рис. 22. Определение порядка точки ЭК
Как можно увидеть на рис. 20, после прохождения всех условий, есть некая функция, которая называется result. Рассматриваемая функция отвечает за генерацию точек ЭК. Это можно наблюдать на рис. 21. В этой функции проверяется кривая на наличие особых кривых, когда значение дискриминанта меньше либо равно 0. Затем, если рассматриваемая ЭК не является особой, то генерируются точки ЭК и выводятся на экран пользователю.
На рис. 22 изображена функция, в которой используются введенные пользователем значения точки ЭК, в результате чего формируется вывод порядка точки, нажав на кнопку, которая представлена на рис. 9.
После определения порядка точки, на рис. 23–24 представлены фрагменты программного кода, которые отвечают за ввод пользователем полинома и вывода полученного регистра на экран, в результате нажатия на кнопку, которая представлена на рис. 12.

Рис. 23. Фрагмент кода, отвечающий за вывод регистра сдвига на экран
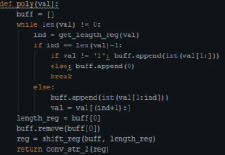
Рис. 24. Программный код, в результате которого формируется регистр сдвига
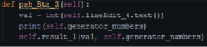
Рис. 25. Функция вывода значения на экран
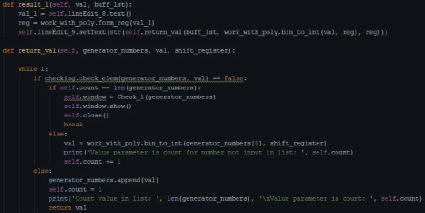
Рис. 26. Фрагмент кода, отвечающий за формирование ПСЧ
Из рис. 25 можно просмотреть функцию, которая по начальному значению, а именно по порядку точки ЭК, выводит каждое последующее уникальное значение ПСЧ, которое основано на регистре сдвига с линейной обратной связью, нажав на кнопку, показанную на рис. 14.
Затем за получение ПСЧ, или сгенерированной последовательности, отвечает функция, которая представлена на рис. 26. Рассматриваемая функция включает в себя проверку полученного значения с теми, которые уже присутствуют в сгенерированной последовательности. Если данное число присутствует, то анализируется последующее полученное число, в результате воздействия регистра сдвига. Если уже все числа – конечны и невозможно получить уникальное значение, которое может включать в себя генератор ПСЧ, то выводится сообщение, как показано на рис. 16, в результате чего можно просмотреть сгенерированную последовательность.
И, наконец, на рис. 27 проиллюстрирована функция, отвечающая за завершение работы программы.
Рис. 27. Функция завершения работы программы
Исследование показателей сгенерированных ПСЧ относительно выбранного многочлена
В рамках эксперимента для улучшения наглядности результатов значения параметров ЭК выбирались одинаковыми. Стоит принять во внимание тот факт, что в основе формирования генератора ПСЧ на основе порядка точки ЭК лежит многочлен. Таким образом, в качестве исследования выбирались несколько различных полиномов.
На рис. 28 приведена зависимость полученного ПСЧ относительно временного промежутка, то есть в определенный момент после нажатия на кнопку, показанную на рис. 14, генерировалось случайное число. Выбирается полином вида: x10 + x7 + x5 + x + 1 и при помощи программного средства формируется генератор ПСЧ.
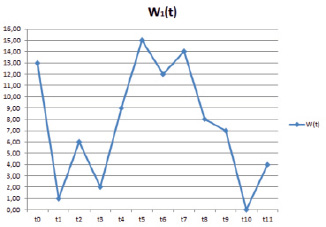
Рис. 28. График зависимости ПСЧ от времени
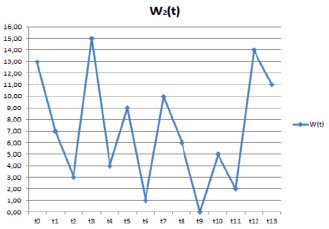
Рис. 29. График зависимости ПСЧ от времени
В качестве W выступает последовательность случайных чисел, а t – временной промежуток.
На рис. 29 представлена зависимость ПСЧ от времени, но отличие состоит в том, что многочлен имеет следующий вид: x5 + x4 + x3 + x.
Таким образом, можно сделать вывод, что при различных полиномах ПСЧ генерируются в определенный момент времени по некоторому закону распределения, основанного на первоначальном значении, в качестве которого выбирается порядок точки ЭК.
В виде закона распределения выступает регистр сдвига с линейной обратной связью.
Заключение
Программа, которая была разработана в ходе статьи, позволяет:
1) определять корректность введенных значений;
2) удобно работать пользователю;
3) формировать ПСЧ на основе первоначального значения в виде порядка точки и регистра сдвига с линейной обратной связью;
4) проводить исследования при формировании генератора ПСЧ.
Библиографическая ссылка
Буковшин В.А., Чуб П.А., Черкесова Л.В. АЛГОРИТМ ФОРМИРОВАНИЯ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ НА ОСНОВЕ РЕГИСТРА СДВИГА С ЛИНЕЙНОЙ ОБРАТНОЙ СВЯЗЬЮ С ИСПОЛЬЗОВАНИЕМ ПОРЯДКА ТОЧКИ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ // Научное обозрение. Технические науки. 2020. № 6. С. 17-25;URL: https://science-engineering.ru/ru/article/view?id=1321 (дата обращения: 11.03.2026).


 science-review.ru
science-review.ru