science-review.ru
Быстродействие электронных устройств, определяющих скорость передачи и обработки информации, ограничено скоростями порядка 40 Гбит/с, поэтому дальнейшее увеличение скорости передачи сигналов по одному каналу требует использования оптических методов [1]. При создании магистральных линий связи на большое число каналов используются возможности, открываемые спектральным уплотнением или мультиплексированием по длинам волн (WDM – Wavelength Division Multiplexing) [2, 3]. Принцип работы заключается в том, что в волоконную оптическую линию связи одновременно вводится излучение от нескольких передатчиков, работающих на разных длинах волн, а на приёмном конце с помощью оптических фильтров происходит разделение сигналов. Для объединения и разделения оптических несущих могут использоваться различные типы мультиплексоров, работа которых основана на различных известных явлениях физической оптики: дисперсии, дифракции, интерференции [4, 5]. Применяемые в линиях связи и телекоммуникационных системах мультиплексоры и демультиплексоры должны вносить малые потери, а мультиплексоры, кроме того, обеспечивать высокую степень изоляции между каналами (высокий уровень развязки). В используемых в настоящее время системах мультиплексирования используются высококачественные, но не регулируемые элементы оптики: оптические призмы, дифракционные решетки, брегговские решетки [6]. Необходимость оперативной перестройки структуры мультиплексоров возникает по разным причинам. Некоторые из них: перераспределение потоков данных в сети в связи с вводом в действие новых узлов, исключением старых, адаптация к неисправностям. Отсутствие возможности перестройки, сложность юстировки определяет высокую стоимость устройств и высокую трудоемкость производства. Использование дисперсионных свойств материалов, чистота которых резко повысилась в последнее время, дает возможность создать новые устройства с высокой скоростью управления параметрами. Связь между магнитной и электрической подсистемами в ферритах и ферроиках, проявляющаяся в виде магнитоэлектрических эффектов, дает возможность с помощью магнитных или электрических полей управлять магнитными свойствами материала и параметров устройств на их базе. Анизотропные свойства материалов дают большие возможности для управления волновыми процессами и создания новых приборов [7]. В последнее время, благодаря появлению новых материалов, стали активно исследоваться вопросы магнитооптики, появились новые устройства магнитооптики. Использование гиротропных сред в оптическом диапазоне в настоящее время ограничивается эффектом Фарадея (модуляторы, выключатели, фазовращатели и др.). На основе монокристаллических магнитооптических пленок ферритов-гранатов с повышенным содержанием висмута и разными типами магнитной анизотропии разрабатываются устройства управления световыми потоками в оптических информационных системах (оптические модуляторы и переключатели). Приборы на основе этого эффекта имеют достаточно большие размеры и не могут быть выполнены методами интегральной технологии. В настоящей работе предлагается метод управления мультиплексированием за счет использования эффекта управления параметрами отражения и прохождения сигнала через границу раздела диэлектрик – подмагниченный феррит. Это позволяет создать новые устройства управления, в том числе в интегральном исполнении. Использование гиротропных материалов в виде тонких пленок ферритов позволяет достаточно просто реализовать управляемое внешним магнитным полем демультиплексирование в интегральных оптических схемах.
Моделирование и основные соотношения
Рассмотрим для примера падение волны поляризации Н (Hx, Hy, Ez) в плоскости x0y на границу раздела феррит – диэлектрик в прямом и в обратном направлениях. При подмагничивании вдоль координатной оси 0z, перпендикулярной плоскости падения, не происходит преобразование поляризации волн и может быть получено аналитическое решение. Параметры феррита характеризуются диэлектрической проницаемостью εf (изотропной) и тензором магнитной проницаемости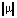 
[7–8]:
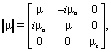
с компонентами тензора: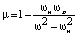 
, 
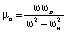, μz = 1, 
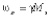, Ms – величина намагниченности насыщения, 
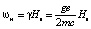– частота резонанса, H0 – величина поля подмагничивания, g ≈ 2 – фактор спектроскопического расщепления. Изотропный диэлектрик имеет параметры диэлектрической проницаемости ε2 и магнитной проницаемости μ2 = 1.
Из уравнений Максвелла следует, что волновые уравнения для H (Hx, Hy, Ez) волн в подмагниченном вдоль координатной оси 0z феррите и в диэлектрике имеют вид
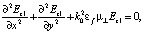
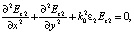
где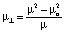 
– поперечная магнитная проницаемость. С учётом частотной зависимости 
.
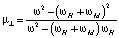Основные результаты и обсуждение
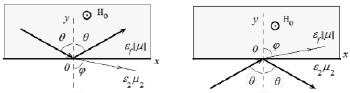
а) б)
Рис. 1. Прохождение луча через границу феррит – диэлектрик
Учет граничных условий в плоскости раздела сред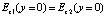 
приводит к обобщенному соотношению Снеллиуса. Оно связывает углы падения θ, преломления φ (рис. 1, a, б) и параметры граничащих сред, которое для структуры, показанной на рис. 1, a, можно представить в виде
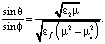
При полном внутреннем отражении (ПВО) угол преломления φ → π/2. В этом случае угол полного внутреннего отражения для границы феррит – диэлектрик определяется соотношением
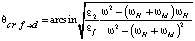
и зависит от величины поля подмагничивания и намагниченности феррита [8]. Отсюда следует, что при падении волны из феррита на границу с диэлектриком полное внутреннее отражение наблюдается в области прозрачности феррита, которая наблюдается в диапазонах частот вне области частот ферримагнитного резонанса (ФМР):
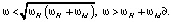
В случае если, наоборот, волна падает из диэлектрика на границу раздела с ферритом, то угол полного внутреннего отражения определяется в виде
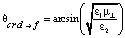
или
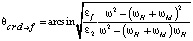
и полное внутреннее отражение наблюдается при условии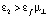 
, если 
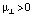, т.е. в области частот (или полей подмагничивания). Наблюдается невзаимность структуры по эффекту ПВО. Для прямых и обратных волн эффект ПВО наблюдается в разных диапазонах частот. Отметим, что явление ПВО на границе раздела диэлектрик – феррит существует только в узких диапазонах частот в области ФМР (рис. 2). Также зависит от намагниченности феррита, от величины поля подмагничивания и соотношения диэлектрических проницаемостей сред (εf /ε2). Наиболее сильная зависимость критического угла эффекта ПВО от величины поля подмагничивания наблюдается в области ФМР.
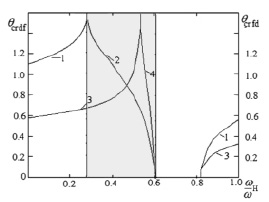
Рис. 2. Зависимость критических углов полного внутреннего отражения при прохождении волны через границу раздела сред феррит – диэлектрик (кривые 1 – εf /ε2 = 1,5, 3 – εf /ε2 = 4) и через границу диэлектрик-феррит (кривые 2 – εf /ε2 = 1,5, 4 – εf /ε2 = 4) в зависимости от нормированного параметра частоты
Явление полного внутреннего отражения на границе раздела диэлектрик – феррит существует только в узких диапазонах частот (для εf /ε2 = 1,5 область выделена на рисунке серым цветом). В области частот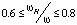 
эффект ПВО не наблюдается в любом случае.
Разложение спектра при отражении и прохождении волны через пленку
Рассмотрим прохождение луча через ферритовую пленку (рис. 3). Угол преломления прошедшего границу раздела сред луча φ и его смещение ? зависит от толщины пленки d показателей преломления граничащих с пленкой сред и параметров ферритовой пленки. Влияние дисперсии параметров пленки приводит к разделению частотных составляющих спектра сигнала (рис. 4).
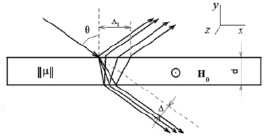
Рис. 3. Разложение спектра при отражении и прохождении волны через пленку
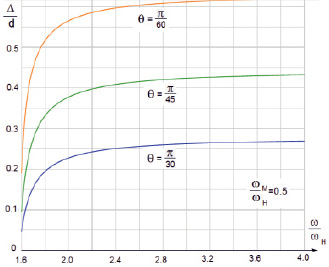
Рис. 4. Нормированное на толщину пленки смещение прошедшего луча в зависимости от нормированной на резонансную частоту поля подмагничивания (ε2 = 1, εf = 4)
Смещение ? луча, прошедшего через пленку толщиной d при угле падения θ, определяется соотношением (ε2 = 1, μ2 = 1):
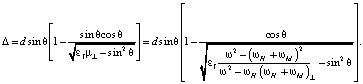
Для отраженного луча его смещение за счет взаимодействия с пленкой определяется соотношением:
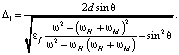
Таким образом, величиной смещения отраженных от пленки и прошедших через пленку лучей можно управлять с большой скоростью меняя угол падения θ и величину поля подмагничивания H0.
На рис. 4 показано изменение относительной величины смещения луча нормированной на толщину пленки, прошедшего через пленку, от отношения параметра отношения частоты сигнала к резонансной частоте. При фиксированной частоте сигнала этот график позволяет оценить зависимость смещения луча от величины поля подмагничивания (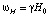
). Относительное смещение луча возрастает с увеличением угла падения θ. Из графиков видно, что наиболее существенно величина магнитного поля влияет на смещение луча в области больших полях подмагничивания при любых углах падения. С ростом угла падения смещение луча уменьшается. Величина смещения имеет порядок толщины пленки и легко обнаруживается экспериментально.
Аналогичная зависимость смещения луча от величины поля подмагничивания наблюдается и в области низких частот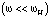 
.
Таким образом, тонкие пленки феррита, имея существенные преимущества в технологии изготовления, могут эффективно использоваться в интегральных устройствах мультиплексирования и демультиплексирования. Полученные результаты могут быть обобщены на случай других материальных сред, обладающих гиротропией [9].
Заключение
Создание эффективных элементов управления оптическими элементами является важной задачей оптоэлектроники. Ферриты могут эффективно использоваться для управления параметрами мультиплексоров и демультиплексоров, обеспечивая высокую скорость управления, ограниченную только скоростью перестройки магнитной системы. Получены соотношения с учетом параметров гиротропных сред и показана зависимость угла прохождения границы раздела сред и угла прохождения гиротропной пленки от величины поля подмагничивания. Определены условия полного внутреннего отражения и зависимость угла полного внутреннего отражения от величины поля подмагничивания. Подмагничивание позволяет менять угол полного внутреннего отражения в широких пределах величиной магнитного поля. На границе раздела феррит – диэлектрик эффект полного внутреннего отражения реализуется для прямых и обратных волн в различных диапазонах частот.
Библиографическая ссылка
Глущенко А.Г., Глущенко Е.П., Иванников А.П. ИСПОЛЬЗОВАНИЕ ФЕРРИТОВ В УПРАВЛЕНИИ ДЕМУЛЬТИПЛЕКСИРОВАНИЕМ // Научное обозрение. Технические науки. – 2021. – № 1. – С. 53-57;URL: https://science-engineering.ru/ru/article/view?id=1337 (дата обращения: 03.12.2024).