science-review.ru
Цель обнаружения объекта – определить, существует ли объект на изображении, и если да, то в каком месте изображения он встречается. Доминирующим подходом к этой проблеме в последнее десятилетие была парадигма скользящих окон, в которой классификация объектов выполняется в каждом месте и в любом масштабе изображения [1]. Недавно была предложена альтернативная структура для обнаружения объектов. Вместо поиска объекта в каждом местоположении и масштабе изображения сначала генерируется набор предложений ограничивающей рамки объекта с целью сокращения набора позиций, которые необходимо дополнительно проанализировать [2]. Замечательное открытие, сделанное вышеперечисленными подходами, состоит в том, что предложения объектов могут быть точно созданы способом, который не зависит от типа обнаруживаемого объекта [3].
Высокая отзывчивость и эффективность – важнейшие свойства генератора предложений объекта [4]. Если предложение не генерируется в непосредственной близости от объекта, этот объект не может быть обнаружен. Эффективный генератор способен обеспечить высокую степень отзыва с использованием относительно небольшого количества ограничивающих рамок кандидатов, обычно от сотен до нескольких тысяч на изображение.
Цель исследования: описать модель пограничных блоков, используемый алгоритм для процесса поиска объекта на изображении. Описать различия между классическими моделями поиска объекта на изображении, а также показать особенности метода пограничных блоков, его сильные и слабые стороны.
Разбор модели пограничных блоков. Предложения по объектам ранжируются на основе единой оценки, рассчитанной на основе контуров, полностью заключенных в ограничивающую рамку кандидата [5]. Все начинается с описания структуры данных, основанной на группах ребер, которая позволяет эффективно отделить контуры, полностью заключенные в рамку, от контуров, которые выходят за ее пределы. Затем определяется функция оценки на основе ребер. Наконец, детализируется подход к поиску предложений по объектам с самым высоким рейтингом, в котором используется структура скользящего окна, оцениваемая по положению, масштабу и соотношению сторон, с последующим уточнением с использованием простого грубого поиска [6].
Учитывая изображение, сначала вычисляется краевой отклик для каждого пикселя. Отклики краев обнаруживаются с помощью детектора структурированных краев, который показал хорошую производительность при прогнозировании границ объекта и в то же время очень эффективен [7]. Используется одномасштабный вариант с улучшением резкости, чтобы сократить время выполнения. Учитывая плотные отклики краев, выполняется не максимальное подавление (NMS), ортогональное отклику края на пики края, рис. 1. Результатом является карта разреженных краев, где каждый пиксель p имеет величину края mp и ориентацию θp. Края определяются как пиксели с mp > 0.1. Контур определяется как набор ребер, образующих когерентную границу, кривую или линию.
Рис. 1. Примеры, показывающие (сверху вниз) первоначальное изображение, структурированные части, сгруппированные части, правильные окно ограничения и маркировка краев и неправильные
Пограничные группы и индекс соответствия. Как показано на рис. 1, цель – идентифицировать контуры, которые перекрывают границу ограничивающего прямоугольника и поэтому вряд ли принадлежат объекту, содержащемуся в ограничивающем прямоугольнике. Для данного блока b мы идентифицируем эти ребра, вычисляя для каждого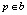 
с mp > 0.1 его максимальное число с ребром на границе блока. Интуитивно понятно, что ребра, соединенные прямыми контурами, должны иметь большее значение, тогда как те, которые не соединены или не соединены контуром с высокой кривизной, должны иметь меньшее значение. Для вычислительной эффективности было обнаружено, что выгодно группировать ребра, которые имеют большее значение, и вычислять только единицы между группами ребер. Далее формируются группы ребер, используя простой жадный алгоритм, который объединяет 8-соединенные ребра до суммы их ориентации, где разница превышает пороговое значение (π/2). Небольшие группы объединяются с соседними группами. Иллюстрация групп кромок показана на рис. 1 в строке 3.
Учитывая набор групп ребер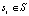 
, вычисляется число между каждой парой соседних групп. Для пары групп si и sj индекс соответствия вычисляется на основе их средних положений xi и xj и средних ориентаций i и j. Интуитивно понятно, что группы ребер имеют большее число, если угол между средними значениями групп аналогичен ориентации групп. В частности, вычисляется индекс соответствия 
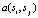, используя
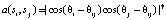, (1)
где θij – угол между xi и xj. Значение γ может использоваться для настройки чувствительности индекса соответствия к изменению ориентации, на практике γ = 2. Если две группы краев разделены более чем на 2 пикселя, их значение равно нулю. Для повышения вычислительной эффективности сохраняются только значения выше небольшого порога (0,05), а остальные принимаются равными нулю [8].
Оценка ограничивающей рамки. Учитывая набор групп ребер S и их индекс соответствия, можно вычислить оценку предложения объекта для любого ограничивающего прямоугольника b-кандидата. Чтобы определить оценку, сначала вычисляется сумма величин mp для всех ребер p в группе si. Также выбирается произвольная позиция xi некоторого пикселя p в каждой группе si. Далее станет ясно, что точный выбор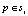 
не имеет значения.
Для каждой группы si мы вычисляем непрерывное значение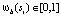 
, которое указывает, содержится ли si полностью в b, 
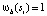или нет, 
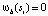. Пусть Sb будет набором групп ребер, которые перекрывают границу бокса b. Необходимо найти Sb, используя эффективную структуру данных, представленную на рис. 2. Для всех 
, 
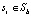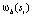устанавливается значение в 0. Аналогично 
для всех si, для которых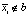 
, так как все его пиксели должны либо находиться вне b, либо 
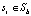. Для остальных групп ребер, для которых 
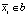и 
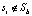, вычисляется 
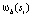следующим образом:
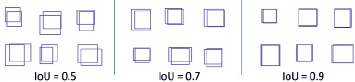
Рис. 2. Примеры случайных ограничивающих прямоугольников
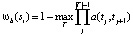, (2)
где T – упорядоченный путь групп ребер длиной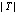 
, который начинается с некоторого 
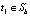и заканчивается на 
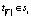. Если такого пути не существует, определяется 
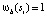. Таким образом, уравнение (2) находит путь с наибольшим индексом соответствия между группой ребер si и группой ребер, которая перекрывает границу окна. Используя вычисленные значения ωb, определяется нужная оценка следующим образом:
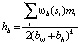, (3)
где bω и bh – ширина и высота бокса. Также следует обратить внимание, что деление происходит по периметру окна, а не по его площади, так как края имеют ширину в один пиксель независимо от масштаба. Тем не менее значение k = 1.5 используется для компенсации смещения больших окон, имеющих в среднем больше краев.
На практике используется интегральное изображение, чтобы ускорить вычисление числителя в уравнении (3). Интегральное изображение используется для вычисления суммы всех mi, для которых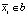 
. Затем для всех si с 
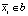и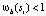 
из этой суммы вычитается 
.
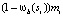Поиск пересекающихся групп ребер. В предыдущем разделе предполагалось, что известен набор групп ребер sb, которые перекрывают границу блока b. Поскольку оценивается огромное количество ограничивающих прямоугольников, эффективный метод поиска sb имеет решающее значение. Простые подходы, такие как исчерпывающий поиск всех пикселей на границе поля, были бы непомерно дорогими, особенно для больших блоков [9, 10].
Существует эффективный метод поиска пересекающихся групп ребер для каждой стороны ограничивающего прямоугольника, основанный на двух дополнительных структурах данных [11]. Ниже описывается процесс поиска пересечений вдоль горизонтальной границы от пикселя (c0, r) до (c1, r). С вертикальными границами можно работать аналогичным образом. Для горизонтальных границ создаются две структуры данных для каждой строки изображения. В первой структуре данных хранится упорядоченный список Lr индексов группы ребер для строки r. Список создается путем сохранения порядка, в котором группы ребер располагаются вдоль строки r. Индекс добавляется к Lr только в том случае, если индекс группы краев изменяется от одного пикселя к другому. В результате размер Lr намного меньше ширины изображения. Если между группами краев есть пиксели, которые не являются краями, в список добавляется ноль. Создается вторая структура данных Kr с таким же размером, как ширина изображения, которая сохраняет соответствующий индекс в Lr для каждого столбца c в строке r. Таким образом, если пиксель p в местоположении (c, r) является членом группы краев si,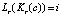 
. Поскольку большинство пикселей не принадлежат группе краев, используя эти две структуры данных, можно эффективно найти список перекрывающихся групп краев, выполняя поиск Lr от индекса Kr(c0) до Kr(c1).
Поиск стратегии. При поиске предложений по объектам следует учитывать алгоритм обнаружения объекта. Некоторые алгоритмы обнаружения могут требовать предложения объектов с высокой точностью, в то время как другие более терпимы к ошибкам при размещении ограничивающей рамки. Точность ограничивающего прямоугольника обычно измеряется с помощью метрики «Пересечение по объединению» (IoU). IoU вычисляет пересечение прямоугольника-кандидата и основного прямоугольника истинности, деленное на площадь их объединения. При оценке алгоритмов обнаружения объектов порог IoU, равный 0,5, обычно используется для определения правильности обнаружения. Однако, как показано на рис. 2, оценка IoU 0,5 является довольно слабой. Даже если предложение объекта сгенерировано с IoU 0,5 с достоверностью, алгоритм обнаружения может дать низкую оценку. В результате обычно желательны оценки IoU более 0,5.
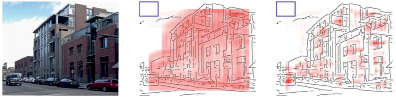
Рис. 3. Пример (оригинальный рисунок слева) оценки с использованием (в центре) и удалением (справа) контуров, перекрывающих границу ограничивающего окна
Необходимо описать стратегию поиска предложения объекта на основе желаемого IoU, ∂, для детектора. Для больших значений ∂ создается более концентрированный набор ограничивающих рамок с более высокой плотностью. Для мелких значений ∂ окна могут иметь большее разнообразие, поскольку предполагается, что детектор объектов может учитывать умеренные ошибки в расположении окон. Важно, что предыдущие методы имеют неявные предубеждения, для которых ∂ предназначены, например Objectness и Randomized Prim настроены на низкий и высокий показатель ∂ соответственно, тогда как в данном случае обеспечивается явный контроль над разнообразием по сравнению с точностью.
Начинается поиск возможных ограничивающих рамок с помощью скользящего окна поиска по положению, масштабу и соотношению сторон. Размер шага для каждого определяется с использованием одного параметра α указывающего IoU для соседних блоков. То есть размеры шага при перемещении, масштабе и соотношении сторон определяются таким образом, что один шаг приводит к тому, что соседние блоки имеют IoU, равное α. Значения масштаба варьируются от минимальной области блока ∂ = 1000 пикселей до полного изображения. Соотношение сторон от 1/τ до τ, где τ = 3 используется на практике. Значение α = 0.65 идеально подходит для большинства значений ∂. Однако, если требуется высокая точность ∂ > 0.9,можно увеличить до 0,85.
После выполнения поиска в скользящем окне все местоположения ограничивающего прямоугольника с оценкой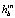 
выше небольшого порога уточняются. Уточнение выполняется с помощью жадного итеративного поиска, чтобы максимизировать 
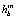по положению, масштабу и соотношению сторон. После каждой итерации шаг поиска сокращается вдвое. Поиск останавливается, когда размер шага перевода меньше 2 пикселей.
После того как ограничивающие прямоугольники-кандидаты улучшены, их максимальные оценки записываются и сортируются. Заключительный этап выполняет не максимальное подавление (NMS) отсортированных окон. Окно удаляется, если его IoU больше, чем у окна с большим количеством значений. Было обнаружено, что на практике установка β = ∂ + 0.05 обеспечивает высокую точность по всем значениям ∂.
Заключение
В данной статье была рассмотрена классическая модель работы поиска объектов с помощью скользящих окон, описана модель пограничных блоков для распознавания объектов на изображении и используемый для этого алгоритм поиска. Также были описаны различия между классическими моделями поиска объектов на изображении и показаны плюсы и минусы описываемого в статье метода.
Библиографическая ссылка
Титова А.А., Козина А.В., Белов Ю.С. МОДЕЛЬ ПОГРАНИЧНЫХ БЛОКОВ ДЛЯ РАСПОЗНАВАНИЯ ОБЪЕКТОВ // Научное обозрение. Технические науки. – 2021. – № 3. – С. 61-65;URL: https://science-engineering.ru/ru/article/view?id=1359 (дата обращения: 24.04.2024).