science-review.ru
В связи с широким проникновением искусственного интеллекта (ИИ) в различные сферы для моделирования когнитивной деятельности человека интерес представляет исследование сложности решения задач в зависимости от вида предметной области (ПО), в которой они формулируются. Чтобы установить такую связь, в первую очередь следует определить параметры, от которых зависит сложность ПО. Естественно, что это определяется формулируемой задачей, поскольку в одной ПО можно сформулировать несколько задач, и сложность их решения не всегда определяется сложностью формулировки. Встречаются просто формулируемые задачи со сложным решением, и наоборот. В связи с этим желательно иметь универсальный показатель сложности задачи в конкретной ПО, который определял бы сложность ее решения. Как представляется, такой показатель должен быть связан с содержательной сложностью задачи независимо от краткости или громоздкости ее формулировки. В настоящей статье предлагается подход, позволяющий ввести показатель сложности задачи с опорой на ее содержательную формулировку.
Полагаем, что O есть множество объектов ПО. Каждый из них однозначно характеризуется конечным набором признаков. Например, это могут быть множество логических матриц с фиксированным значением n строк и m столбцов или множество образов, заданных своими элементами, где каждый элемент принадлежит конечному алфавиту. Одновременно с множеством O рассматривается множество O* так называемых недоопределенных объектов, каждый из которых содержит лишь часть наборов признаков, характеризующих объекты. Например, если в качестве объектов рассматриваются матрицы с n строками, то в качестве недоопределенных объектов можно рассматривать матрицы с n1 < n строками. Если объекты – это некоторые образы, то недоопределенные объекты – суть их собственные части. Понятно, что каждый недоопределенный объект можно доопределить, в общем случае, разными способами до объекта ПО. Будем полагать, что если недоопределенный объект o* доопределяется до объекта o, то это происходит в результате конкатенации o* с некоторым недоопределенным объектом o1*, что будем обозначать o = o*o1*. Введем пустой недоопределенный объект λ, который можно доопределить до любого объекта. Однако для объекта или недоопределенного объекта o верно равенство o = oλ. Поэтому полагаем, что справедливо включение O⊂O*. И в дальнейшем будем употреблять общий термин объект, выделяя недоопределенные объекты по мере необходимости.
Полагаем, что решаемая задача Z над ПО с множеством O объектов состоит в установлении некоторого свойства P над O. Поэтому задача Z определяет на множестве O* отношение эквивалентности объектов o1, o2∈O*(o1 ≈ o2 ⇔ ∀o*∈O*(o1o, o2o∈O ⇒ P(o1o) = P(o2o))). Однако два недоопределенных объекта o1, o2∈O* называются разделяемыми, если выполняется соотношение: ∃o*∈O*(o1o*, o2o*∈O ⇒ P(o1o*) ≠ P(o2o*))). В этом случае o* называется разделяющим объектом.
Каждый класс эквивалентности определяет свою собственную подзадачу, которую необходимо решить, чтобы получить искомое решение общей задачи. В логике это называется разбором случаев. Например, задачу над множеством целых чисел можно представить как две задачи: одна предполагает рассматривать четные числа в качестве новой ПО, другая – нечетные. Другой пример: решение числовых головоломок. В процессе решения происходит разбор случаев, каждый характеризуется уникальной комбинацией замен букв цифрами и требует своего решения. Поэтому исходная задача представляется совокупностью подзадач, решение которых приведет к окончательному результату.
Все отношения эквивалентности, которые можно ввести над множеством объектов ПО, образуют частично упорядоченное множество, по включению. Чем слабее эквивалентность, тем уже ее классы эквивалентности, т.е. тем слабее условия, при которых объекты эквивалентны. Самая сильная подразумевает эквивалентность всех объектов ПО. Самая слабая характеризуется классами, состоящими из одного объекта. В этом случае бессмысленно говорить о какой-либо связи объектов, задача не имеет содержательного смысла.
Для решения нетривиальной задачи над ПО обязательно наличие априорной информации о факторизации множества объектов. Это устраняет неопределенность, неизбежную при поиске решения и связанную с объединением в классы семантически совпадающих объектов. Чем сильнее отношение эквивалентности, т.е. чем шире ее классы, тем больше неопределенности устраняется при решении и тем компактнее решение. Например, при решении геометрической задачи, чем большим числом доказанных соотношений между фигурами располагаем, тем шире классы эквивалентности фигур на чертеже. И, как следствие, тем компактнее решение, так как всякое неизвестное, но обязательное для решения соотношение надо доказывать.
Пусть π есть всюду определенная арифметическая программа, вычисляющая предикат P. Если на ее вход поступает объект o∈O, то программа завершает работу в точности в одном из двух финальных состояний: c0 либо c1, в зависимости от значения P(o), соответственно 0 или 1. Если на вход программы поступает недоопределенный объект o*, то он определяет одно вычисление π(o*), заканчивающееся в некотором, в общем случае, не финальном состоянии c*. Поскольку π всюду определенная, то если на ее вход поступает любой объект, то ее вычисление завершается в некотором состоянии. Однако каждое вычисление программы π вызывается некоторым объектом o*. Это вычисление может быть продолжено за счет различных вычислений, которые получаются, если объект o* доопределять различными способами.
Следующим образом введем отношение π-эквивалентности: для объектов o1, o2∈O*(o1 ≈ πo2 ⇔ ∀o*∈O*(o1o*, o2o*∈O ⇒ вычисления π(o1o*) и π(o2o*) заканчиваются в одном состоянии). Очевидно, что для эквивалентных объектов из O финальные состояния совпадают. Отметим, что состояния, в которых завершаются вычисления π(o1) и π(o2), могут быть различными. Но при всяком одинаковом продолжении o* объектов o1 и o2 до полностью определенных объектов эти продолжения заканчиваются всегда в одинаковом состоянии, т.е. объекты o1o* и o2o* одновременно либо обладают, либо не облают свойством P. В результате получаем следование: ∀o1o2∈O*(o1 ≈ πo2 ⇒ o1 ≈ o2).
Покажем, что верно и обратное следование. Пусть два недоопределенных объекта o1, o2∈O* находятся в отношении o1 ≈ o2, и вычисления π(o1) и π(o2) заканчиваются в состояниях соответственно c1 и c2. Допустим, что имеется такое продолжение o*, что o1o*, o2o*∈O, но из этих двух состояний c1 и c2 можно продолжить вычисления в разные финальные состояния. Следовательно, имеется одно продолжение для эквивалентных объектов, которое переводит два состояния c1 и c2 в два разных финальных состояния. Следовательно, продолжение o* – разделяющее, поэтому объекты o1, o2 не эквивалентные. Это противоречие. Следовательно, верно соотношение: ∀o1o2∈O*(o1 ≈ o2 ⇒ o1 ≈ πo2).
Полагаем, что каждый объект из множества O представляется бинарным вектором, а недоопределенные объекты представляются векторами над базисом <0, 1, _>. Здесь символом _ обозначены неизвестные или несущественные признаки. Поэтому все объекты ПО можно представить в виде бинарного дерева T с единственным корнем, в котором каждый узел имеет двух непосредственных потомков, один порождается дугой с меткой 0, другой – 1. Каждый путь из корня описывает в точности один, в общем случае, недоопределенный объект. Пути из корня, заканчивающиеся в висячих узлах, определяют объекты из множества O.
Теперь, если в бинарном дереве ввести склейку узлов, представляющих один класс, то сила эквивалентности определяет число склеек. Чем сильнее эквивалентность, тем больше склеек в дереве. В результате висячие узлы любого поддерева, содержащего корень, представляют классы, объекты которых определяются путями, ведущими в один узел. А все пути, ведущие в один узел, определяют один класс. Последний определяет подзадачу, решение которой необходимо в рамках общего решения задачи. Однако невозможно ввести числовой параметр, который измерял бы силу априорно известной эквивалентности объектов ПО, поскольку эквивалентности образуют частично упорядоченное множество по включению. Тем не менее, силу эквивалентности можно охарактеризовать количеством склеек в бинарном дереве: чем больше склеек, тем эквивалентность сильнее.
Поскольку один узел определяет класс эквивалентности объектов, то сечение C дерева T определяет классы эквивалентности объектов, характеризующихся фиксированными наборами параметров. Тогда множество C определяет вычисления программы π, оканчивающиеся, по меньшей мере, в |C| различных состояниях. Для кодирования этих состояний в программе π требуется память не меньшая, чем log2|C| бит [1–4]. Однако все объекты из C не могут быть закодированы c меньшей, чем log2|C|, сложностью. Следовательно, в программе π имеется вычисление длины не меньше |C|. Так удалось оценить память арифметической программы в зависимости от максимального сечения бинарного дерева, представляющего объекты ПО.
Введем параметр неопределенности бинарного дерева, полагая, что дуги, ведущие из одного узла в непосредственные потомки, равновероятные. Неопределенность в таком случае связана с неопределенностью того, какие подзадачи будут решаться при решении общей задачи. Известно число подзадач, известно частотное распределение, пусть p1, p2, …, pq, объектов ПО, с которым они попадают в q классов, т.е. используются в качестве аргументов подзадач. Следовательно, можно подсчитать неопределенность H совокупности этих классов как характеристику исходной задачи над ПО [5].
Покажем, что так введенная неопределенность может служить параметром, определяющим сложность задачи. Для этого свяжем неопределенность задачи как неопределенность разбиения объектов ПО со сложностью вычислений программы, решающей исходную задачу. Здесь исходим из следующих соображений. Предполагается, что каждый класс определяет совокупность вычислений программы p, решающей исходную задачу, т.е. вычисляющей предикат P. Все вычисления программы представляются так называемой разверткой, т.е. бинарным деревом с единственным корнем, в котором вычислительные узлы не вызывают размножения вычислений, а логические представляются узлами с двумя потомками.
Связь между бинарным деревом разбора объектов ПО и разверткой устанавливается исходя из следующих соображений. Если в бинарном дереве разбора ПО имеются два узла, пусть n0 и n1, определяющие разные классы объектов и, соответственно, различные подзадачи, то им в развертке Rπ программы π соответствуют два различных множества вычислений. Если допустить, что это не так, то приходим к заключению, что эквивалентность, определенную на множестве объектов ПО, можно усилить, объединив классы, соответствующие узлам n0 и n1. В результате каждому поддереву T бинарного дерева разбора объектов ПО в развертке Rp соответствует бинарное дерево вычислений с корнем, такое, что каждый узел n∈T определяет множество Mn вычислений. И разные узлы дерева T определяют разные множества вычислений. Тогда, если H есть неопределенность дерева T, то соответствующее бинарное поддерево развертки Rπ имеет глубину не меньше, чем H, а число различных вычислений не меньше 2H. Так можно оценить как размер памяти программы π, так и число вычислений. Исходя из базиса арифметической программы оценивается сложность вычисления. Так, если базис состоит из логического оператора = и арифметических s(x) – прибавления единицы и 0(x) – обнуления переменной, то средняя длина вычисления, определяемого поддеревом разбора ПО с неопределенностью H, не менее 2H.
Информационные модели. Считаем, что объект управления описывается уравнением y = f(x), где x – это входные параметры, y – демонстрируемое поведение. Тогда его информационной моделью могут служить, например, таблицы базы данных, описывающие его поведение, или программа, вычисляющая функцию f(x), и т.п.
Пример 1. Пусть информационная модель отражает совместимость комплектующих при сборке изделия с заданным функционалом. Если она адекватна, то удастся избежать сборки неправильно функционирующего изделия.
Пример 2. Пусть информационная модель отражает совместимость химических компонентов при синтезе вещества с заданными качествами. Если она не адекватна, то возможен синтез вещества с незапланированными качествами.
Сформулируем некоторые аналогии между понятиями теории информации и введенными представлениями. Передатчику информации соответствует наблюдаемая часть модели, а сигналу – поведение этой части, выраженное в тех или иных терминах. Канал связи соединяет наблюдаемую часть модели с частью, на которую осуществляется воздействие. Приемником информации служит еще не наблюдаемая часть модели, на которую воздействует активная, функционирующая часть. И в зависимости от сигнала приемник переходит в какое-либо состояние.
Пример 3. Пусть M есть логическая матрица размерности [n×m], M = M1 + M2, M1 имеет размерность [n1×m], M2 – [n2×m], n = n + n2. Воздействиями на модель является множество Σ всех означиваний n1 строк матрицы M1. Эта подматрица есть передатчик, который преобразует воздействия в сигналы. Каналом является горизонталь, разделяющая матрицы M1 и M2. Приемником является матрица M2. Каждое воздействие σ∈Σ превращает в истину часть Hσ столбцов матрицы M1. Множество истинных столбцов Hσ есть сигнал, передающийся от передатчика приемника. Приемник реагирует на такой сигнал однозначно, при последующем рассмотрении эти столбцы вычеркиваются из матрицы M2. В результате выходные сигналы канала воздействуют на приемник, изменяя его состояние. Таким образом, воздействия Σ формируют выходные сигналы, а именно множество подматриц матрицы M2.
Здесь под моделью понимается дискретная функция φ:A→B, где A есть множество входных воздействий, B – выходных. Значения ее аргумента x представляют собой бесконечные бинарные слова. Каждое слово представляется конкатенацией конечной префиксной части, заканчивающейся самой правой единицей, и нулевым бесконечным суффиксом. Говорим, что двоичная последовательность, означивающая часть аргументов x, является частичным x-набором. Аналогично будем говорить о частичном y-наборе выходных значений. Анализ поведения функции φ сводится к проверке равенства φ(σx) = σy для всякой пары (σx, σy) соответственно (в том числе частичных) x-набора и y-набора.
Допустим, что при всяком допустимом означивании подмножества x'⊂x входных параметров известна выходная реакция модели. В результате модель φ представляется объединением φ1, φ2, …, φq подмоделей, число которых не больше числа частичных x-означиваний. Следовательно, анализ поведения модели в зависимости от частичных входных параметров x' сводится к двум задачам.
1. Выяснить тип поведения из известных φ1, φ2, …, φq, демонстрируемый при известном входном векторе σx.
2. Исследовать каждую из подмоделей φ1, φ2, …, φq.
Пусть событие A встречается с частотой pA и γ(A) = -log2pA есть показатель его неожиданности, зависящий от частоты pA. Величину γ(A) назовем частной неопределенностью HA события A. Если имеются q различных значений A1, A2, …, Aq одной случайной величины, каждое из которых встречается с частотой соответственно p1, p2, …, pq, то усредненная неопределенность равна H = -Σi=1,qpiγ(Ai).
Если частичный набор σx' означивает часть аргументов x'⊂x, то аргументы x' назовем неподвижными, а оставшиеся – изменяемыми. При означиваниях изменяемых аргументов так, что результирующие наборы принадлежат области определения Def φ, какие-то компоненты y'⊂y могут принимать значения, не меняющиеся при означивании оставшихся компонентов аргумента. В этом случае x-набор σx' определяет функцию φ|σx'(u):
1) переменные u суть изменяемые аргу-
менты;
2) область определения Def φ|σx' получается в результате ограничения области Def φ означиваниями, x'-проекции которых совпадают с σx';
3) функция φ|σx'(u) получается из функции φ при аргументах с фиксированным частичным x-означиванием σx' игнорированием неподвижных y-компонентов.
Пример 4. Пусть σx = 01011 = 2610 есть частичное x-означивание аргументов двоичной функции прибавления единицы: φ(x)=x+1. Полагаем, что младшие разряды располагаются слева. Тогда функция φ|σx'(u) = 25u, поскольку неподвижные компоненты значений функции суть компоненты с нулевого до четвертого включительно, а остальные – изменяемые, и отсутствует перенос в пятый разряд. Все значения функции φ(x) имеют своим префиксом 11011, если ограничить область ее определения двоичными аргументами с префиксом 01011.
Говорим, что x-наборы σ'x и σ"x эквивалентные относительно функции φ, если функции φ|σ'x'(u) и φ|σ"x'(u) совпадают.
Пример 5. Для функции φ(x) = x + 1
означивания: σ'x = 01011, σ"x = 11111, σ'"x = 11011 определяют: φ|σx'(u) = 25u, φ|σx'"(u) = 25u, φ|σx"(u) = 25u+1. Префиксы значений функции φ(x) суть следующие: 11011, если префикс аргумента σ'x; 0000, если префикс σ"x; 00111, если префикс σ'"x. При σ"x возник перенос в пятый разряд, в первом и третьем случаях переноса нет. Поэтому функция φ|σx"(u) отлична от φ|σx'(u) и φ|σx'"(u), наборы σ'x и σ'"x эквивалентны, а σ"x не эквивалентен им.
Эквивалентность x-наборов сводит исследование исходной модели к описанию совокупности подмоделей. Число m классов определяет m различных подмоделей. И, если каждая подмодель предполагает собственное вычисление, то имеется m различных вычислений. Следующий пример демонстрирует содержательные рассуждения и введенные определения.
Пример 6. Пусть π(x) есть двоичная арифметическая программа, представленная своей диаграммой с двумя типами узлов: логических и арифметических. Тогда ее вычисления задаются входными значениями. Под вычислением понимаем последовательность арифметических и логических операторов, выполняющихся при заданном входе до остановки. В результате выходная переменная y принимает определенное значение.
Полагаем, что означивания σ1 и σ2 части x', |x'| = l, аргумента эквивалентные (σ1 ≈ σ2), если определяемые ими вычисления завершаются в одном и том же состоянии. Поэтому вычисления разбиваются на классы, определяемые эквивалентными означиваниями. И каждое частичное означивание определяет подпрограмму, выполняемую после продолжения этого означивания. Пусть π1, π2, …, πq суть выделяемые подпрограммы, множество вычислений, определяющих подпрограмму πi, обладает долей pi, i = 1, 2, …, q среди всех вычислений над частичными входами длины l. Тогда неопределенность вопроса: какое событие из π1, π2, …, πq наступит при означивании σx части x' аргументов, |x'| = l, зависит лишь от долей p1, p2, …, pq, и равна H1 = -Σi=1,qpilog2pi.
Исследование программы как совокупности π1, π2, …, πq подпрограмм, обладающих собственными множествами вычислений, соответственно T1, T2, …, Tq, i = 1, 2, …, q, обладает неопределенностью H2 = Σi=1,qpilog2|Ti'|.
Понятно, что исследование программы приводит к разным значениям неопределенности. Если l = 0, то неопределенность максимальная, поскольку не известны возможные вычисления. Когда известны все вычисления, то неопределенность равна нулю. В случае частичных означиваний, 0 < l < n неопределенность равна сумме H1 + H2.
Обобщим предыдущие рассуждения следующим образом.
Пусть Tree есть растущее вниз однокорневое бинарное дерево, каждый висячий узел которого обозначает некоторый класс эквивалентности объектов ПО, и его энтропия равна H. Полагаем, что введенная эквивалентность определяет семантику ПО, когда одинаковые объекты суть элементы одного класса эквивалентности. Бинарное дерево с минимальной длиной пути из корня в листья и энтропией H имеет глубину H и в точности 2H висячих узлов.
Свяжем энтропию дерева Tree со сложностью вычислительной процедуры, которая не различает эквивалентные объекты, выдавая для них одинаковые ответы. Для этого допустим, что имеется некоторая вычислительная процедура π(x), вычисляющая некоторую двоичную всюду определенную функцию y = f(x) от одного аргумента. Полагаем, что в процессе вычисления процедура π переходит из одного состояния в другое, и ее состояния представляются внутренней памятью, которая есть бинарный вектор неограниченной длины. При отсутствии входа процедура находится в фиксированном нулевом состоянии, когда память заполнена нулями. Каждому состоянию соответствует уникальный вид этого вектора с ненулевым ограниченным префиксом и бесконечным нулевым суффиксом. Каждый вход σ либо приводит к остановке процедуры в финальном состоянии End, либо процедура достигает промежуточного состояния S, из которого она продолжит вычисление при расширении входа новыми компонентами. Тем самым все входные последовательности разбиваются на классы эквивалентности: с каждым классом связано уникальное состояние процедуры, из которого она продолжает вычисление при расширении аргумента. И для разных классов продолжения вычисления различные.
Представим вычисления процедуры π(x) в виде следующего бинарного дерева Tree(π) (развертки). Корнем дерева служит состояние процедуры при пустом входе. Полагаем, что в корень ведет дуга, помеченная пустой меткой. Если некоторый узел n развертки представляет состояние S вычисления, полученное в результате подачи на вход процедуры бинарной последовательности σ, то из него выходят две дуги, помеченные 0 и 1. Каждая из них ведет в узел соответственно n0 и n1, представляющие собой состояния, в которые переходит процедура π при входах соответственно σ0 и σ1. Одинаковые состояния развертки склеиваются.
Пусть на вход процедуры π поступают все бинарные последовательности длины l. Часть ее развертки Tree(π, l), представляющая собой начальное поддерево с длиной ветвей l, определяет эквивалентность на множестве этих входов: два входа эквивалентные, если соответствующие вычисления приводят к одному состоянию. Исходя из этого и полагая равновероятными дуги, ведущие из одного узла развертки и помеченные 0 и 1, подсчитаем энтропию H дерева Tree(p, l). Тогда минимальная глубина двоичного дерева с энтропией H равна H, а число его висячих узлов – 2H.
Так как каждый висячий узел определяет одно состояние вычисления, то состояний внутренней памяти будет не менее 2H. Следовательно, чтобы реализовать все вычисления, представленные деревом Tree(π, l), необходима внутренняя память, содержащая не меньше H компонентов. В противном случае не удастся получить все классы эквивалентности входов процедуры.
В данном случае эквивалентность входов процедуры π определялась исходя из состояний самой процедуры. Также исходя из этого строилась развертка и определялась энтропия частичной развертки. Однако при изучении конкретной ПО нет априорной информации о поведении вычислительной процедуры. Поэтому интерес представляет такое определение эквивалентности над объектами ПО, чтобы разные классы определяли различные вычисления. Тогда по мощности фактор множества можно оценить размер памяти вычислительной процедуры, а затем исходя из особенностей ее вычислительных правил оценить сложность вычислений.
Исходя из этого рассмотрим вопрос, как выглядит неопределенность модели в зависимости от различных определений эквивалентности ее состояний при частичном означивании аргумента. В качестве примера рассмотрим формулу разложения логических функций (по переменной x) f(x) = x∧f(1)∨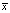
∧f(0), полагая, что логическая функция задана матрицей, представляющей ее КНФ. Тогда разложение по нескольким переменным можно представить бинарным деревом, в котором узлы суть логические матрицы, и при его построении матрицы, определяющие эквивалентные (в каком-либо смысле) функции, склеиваются. Эквивалентности в данном случае могут быть различные. Это могут быть: логическая эквивалентность, совпадение матриц с точностью до перестановки строк и столбцов, логическая эквивалентность, доказываемая за ограниченное число преобразований, буквальное совпадение матриц и т.д. Понятно, что все эквивалентности, не противоречащие формуле разложения, формируют частично упорядоченное множество с минимальным элементом – логической эквивалентностью (самой сильной) и максимальным – буквальным совпадением матриц (самой слабой). При различных эквивалентностях получаются различные бинарные деревья. При более сильной эквивалентности будет больше склеиваний, нежели при слабой.
Пусть при одном порядке переменных разложения исходной функции и при различных эквивалентностях E1 и E2, E1 ≤ E2 получаются два бинарных дерева T1 и T2.
И при одной последовательности y разложения переменных получаются два сечения S1 и S2 бинарных деревьев T1и T2. Тогда энтропии H1 и H2, определяемые сечениями соответственно S1 и S2, находятся в отношении: H1 ≤ H2. Следовательно, более сильная эквивалентность определяет меньшую энтропию, что вполне объяснимо: более сильная эквивалентность за счет более частой склейки узлов в бинарном дереве определяет меньшую энтропию. Содержательно это трактуется следующим образом: эквивалентность, подразумеваемая в разложении функции, устраняет часть неопределенности за счет дополнительных свойств рассматриваемых объектов. Поэтому неопределенность бинарного дерева меньше. Понятно, что так введенная энтропия касается только вида бинарного дерева и не учитывает сложности вычисления эквивалентностей. А поэтому ничего нельзя сказать о реальной сложности вычислений, не располагая знаниями о сложности вычисления эквивалентности.
Библиографическая ссылка
Попов С.В. О СОДЕРЖАТЕЛЬНОЙ ИНФОРМАЦИИ И РЕШЕНИИ ЗАДАЧ // Научное обозрение. Технические науки. – 2021. – № 6. – С. 10-16;URL: https://science-engineering.ru/ru/article/view?id=1374 (дата обращения: 23.11.2024).