science-review.ru
Дифференциальные уравнения второго порядка [1] используются для описания множества физических, технических, биологических, химических, социологических, экономических и прочих видов процессов, явлений или характеристик систем, например движения объектов под действием внешних сил [2], изменения параметров электрических величин, динамики сгорания газообразного топлива, изменения численности популяций или энергии микрочастиц. Представление функции процесса или системы в виде дифференциального уравнения означает, что она изменяется в зависимости от изменения какого-либо параметра или нескольких параметров (чаще всего времени и координат).
Основным из типов решения таких дифференциальных уравнений является так называемая задача Коши [3], состоящая в нахождении основной функции путём интегрирования при некотором заданном наборе начальных условий (чаще всего в момент времени t = 0). Также, как правило, на значения искомой функции накладываются некоторые ограничения по границам рассматриваемой области её определения (задаются так называемые граничные условия) [4].
Самые простые из дифференциальных уравнений второго порядка позволяют найти решение точными математическими методами, однако далеко не все. К счастью, к настоящему времени разработано множество программных продуктов, позволяющих решать такие задачи численными методами, при этом не вдаваясь в подробности функционирования данных методов. Наиболее известными программами, позволяющими решать дифференциальные уравнения, являются MathCAD [5] и MatLab [6], однако они отличаются высокой стоимостью лицензий, а также малым быстродействием.
Альтернативным (и всё более популярным) путём решения дифференциальных уравнений является применение специальных научных библиотек для различных языков программирования, в частности для широко известного свободно распространяемого высокоуровневого языка программирования Python [7]. Данный язык отличается от прочих вычислительных средств простотой освоения и постоянным развитием, появлением всё более совершенных версий библиотек математических функций.
Целью описываемого исследования является разработка методики численного решения дифференциальных уравнений второго порядка, создание на её основе алгоритма и кода программы на языке программирования Python. Результаты решения должны выводиться в наглядной графической форме. Для реализации всех описанных функций программы необходимо использовать специально подобранные для этого библиотеки функций (модули) Python. Далее, написанный код программы необходимо апробировать с помощью рассмотрения конкретного физического явления, описываемого дифференциальным уравнением второго порядка.
В качестве такого явления выбрано изучение одной из задач квантовой механики – движения элементарной частицы, находящейся в так называемой одномерной прямоугольной потенциальной яме [8], имеющей бесконечную глубину (с бесконечно высокими непроницаемыми стенками) (рис. 1).
При движении частицы вдоль оси x в области x = 0…a потенциальная энергия частицы U(x) равна нулю, а при x < 0 и x > a энергия U(x) = ∞.
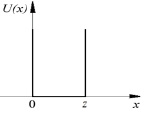
Рис. 1. Прямоугольная потенциальная яма
В результате необходимо получить и изучить так называемую волновую функцию [9] частицы, описывающую чистое состояние (положение) частицы, путём построения графиков волновых функций на разных энергетических уровнях [10]. По графикам можно узнать частоты колебаний частицы (например, электрона) на различных энергетических уровнях. После этого, находя квадрат значения волновой функции, получим графики, характеризующие плотность вероятности нахождения частицы в точке с заданными координатами в данный момент времени для каждого энергетического уровня.
В ходе решения задачи предполагается также найти полную энергию частицы на разных энергетических уровнях (которая постоянна в пределах x = 0…a) и построить графики значений этой энергии. При этом можно выявить особенности движения частицы в прямоугольной потенциальной яме, такие, например, как квантование энергии, вырождение энергетических уровней и т.д.
Материалы и методы исследования
Таким образом, конечным материалом описываемого исследования является разработка кода программы на языке программирования Python, позволяющей решать дифференциальные уравнения второго порядка (содержащие вторую производную от какого-либо параметра). Основным выбранным методом является численное решение на основе библиотеки научных расчётов Scipy для Python, а именно интегрирующей функции Odeint [11] из подмодуля этой библиотеки Scipy.integrate.
Алгоритм разработанной на основе указанных принципов программы состоит из следующих блоков:
1. Загрузка следующих библиотек для языка Python: вышеупомянутого подмодуля Scipy.integrate, модуля Numpy [12] для создания и заполнения массивов данных (результатов расчётов для построения графиков), модуля Math (для использования некоторых математических функций и констант, не содержащихся в языке Python по умолчанию – например, для вызова числа π), подмодуля Matplotlib.pyplot для представления результатов расчётов в виде двухмерных графических зависимостей.
2. Задание исходных данных, представляющих из себя коэффициенты дифференциального уравнения или уравнений, а также начальные и граничные условия.
3. В случае необходимости – определение формул или условий для нахождения дополнительных функций, используемых в конкретных дифференциальных уравнениях.
4. Создание функции, описывающей левые части дифференциальных уравнений первого порядка, полученных после преобразования исходного дифференциального уравнения второго порядка (методика такого преобразования и состав левых и правых частей уравнений будут продемонстрированы далее на примере).
5. Создание главной функции программы, в рамках которой происходит определение двух массивов, которые далее при выполнении цикличных вычислений будут заполнены значениями переменной величины и соответствующей ей функции. Команда определения функции Integrate.odeint включает в качестве аргументов левые части дифференциальных уравнений (п. 4), правые части тех же уравнений (начальные условия) и массив, содержащий значения переменной, при которых следует вычислять функцию.
Далее функция, вычисленная при всех значениях переменной, выводится с использованием графической библиотеки на экран.
6. Вычисление некоторых вспомогательных величин и главной функции, описанной в п. 5 алгоритма.
Далее рассмотрим применение разработанной программы для решения примера из квантовой физики – движение частицы вдоль оси x в пределах изображённой на рис. 1 прямоугольной потенциальной ямы. Данный процесс описывается одномерным дифференциальным уравнением Шредингера:
,
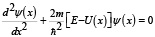где ψ(x) – волновая функция движения частицы;
x – координата положения частицы;
m – масса частицы (так как в качестве примера элементарной частицы мы рассматриваем электрон, то m = 9.10938356·10-31 кг);
? – постоянная Планка, равная 1.054571817·10-34 Дж·с;
E – полная энергия частицы, Дж;
U(x) – потенциальная энергия частицы, Дж.
Как видим, представленное дифференциальное уравнение движения элементарной частицы имеет вторую производную по координате x, а следовательно, относится к классу исследуемых в данной работе зависимостей. Однако для применения в программе его необходимо преобразовать – представить в виде системы двух дифференциальных уравнений первого порядка, что делается при помощи простой замены переменных:
.
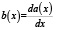Тогда уравнение Шредингера может быть представлено следующим образом (при переносе первого его слагаемого в правую часть):
.
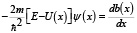Для решения системы из двух представленных дифференциальных уравнений необходимо задаться начальными и граничными условиями задачи.
Начальными условиями являются следующие: при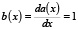 
(можно взять любое постоянное число – единица выбрана для определённости, и она является правой частью первого уравнения системы) 
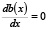(правая часть второго уравнения, проистекающая из рассмотрения уравнения Шредингера).
Граничные условия ясны из рассмотрения рис. 1 и являются начальной и конечной координатами стенок потенциальной ямы: х = 0 и х = z, где z – любое натуральное число. Для определённости в программе использовано значение z = 1000 при шаге вычисления всех параметров системы, равном 1, что вполне достаточно для построения по результатам расчётов плавных графических зависимостей.
Результаты исследования и их обсуждение
Продемонстрируем работу разработанной программы на описанном выше примере – рассмотрении движения элементарной частицы (в качестве которой выбран электрон) в одномерной прямоугольной потенциальной яме.
Для формирования полного набора исходных данных в программу необходимо добавить формулу для полной энергии частицы:
,
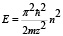где n – целое число, называемое квантовым уровнем энергии частицы. Значение остальных констант, входящих в формулу, приведено выше.
В квантовой теории доказывается, что решение уравнения Шредингера для прямоугольной потенциальной ямы (волновая функция) неравно нулю только при дискретных целых значениях n.
Вычисляя с помощью программы E для электрона при n = 1, 2, 3, 4, 5 и визуализируя полученные значения с помощью Microsoft Excel, получим следующую картину (рис. 2).
Представленная диаграмма наглядно демонстрирует тот факт, что с увеличением квантового уровня n на единицу энергия частицы возрастает всё более стремительно.
На следующем графике (рис. 3) покажем выводимые программой графики волновых функций для двух значений n = 2 и n = 5, а также квадратов волновых функций для тех же n. При вычислениях используются значения E, представленные на рис. 2 и соответствующие текущему n (программа показывает, что при других значениях E волновая функция во всём диапазоне x от 0 до z равна нулю).
Рис. 2. Вычисленные квантовые уровни энергии электрона
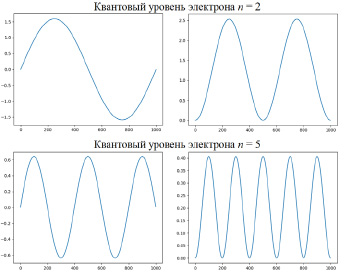
Рис. 3. Графики волновых функций и их квадратов для электрона
Таким образом, по осям абсцисс отложена ширина потенциальной ямы в условных координатах для двух значений квантовых уровней. Правые графики, изображающие изменение квадрата волновой функции ψ2, позволяют судить о вероятности нахождения частицы в разных местах по координате x (по относительному значению по оси ординат). В этом состоит основной физический смысл построения таких функций. В данном случае наглядно видно, что количество координат x, соответствующих максимальной вероятности нахождения электрона, равно номеру рассматриваемого квантового уровня n.
Заключение
Полученные в ходе проведения работы методика и программа решения дифференциальных уравнений второго порядка могут быть использованы в любых подобных рассмотренному случаях с минимальными доработками. Для разных дифференциальных уравнений второго порядка в программе необходимо только прописать свои выражения для правых и левых их частей, а также изменить начальные и граничные условия.
Выводы по результатам решения уравнений можно сделать на основе выводимых программой наглядных графических зависимостей искомой функции от аргумента. Описанная в статье апробация разработанной методики позволяет рекомендовать использовать язык Python совместно с описанными библиотеками функций (главной из которых является модуль Scipy) для решения рассмотренного круга задач благодаря следующим доказанным достоинствам данного подхода:
1) простота кода программы и его модификации под разные задачи;
2) высокая скорость вычислений;
3) наглядная визуализация результатов;
4) бесплатность программных продуктов и их доступность для всех желающих;
5) высокая степень вовлечённости исследователя в процесс формулирования и решения задач, что особенно важно для достижения понимания физико-математических связей в исследуемых проблемах, особенно для начинающих.
С помощью языка Python возможно (и запланировано) дальнейшее совершенствование разработанного программного продукта для решения более сложных классов уравнений, например систем дифференциальных уравнений в частных производных.
Библиографическая ссылка
Ильичев В.Ю., Назаров Е.С. АВТОМАТИЗАЦИЯ РЕШЕНИЯ ЗАДАЧ, ОПИСЫВАЕМЫХ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ ВТОРОГО ПОРЯДКА // Научное обозрение. Технические науки. – 2022. – № 1. – С. 45-49;URL: https://science-engineering.ru/ru/article/view?id=1385 (дата обращения: 23.11.2024).