Индивидуальные спортивные дисциплины предполагают выступление одного спортсмена, оценку его результатов и подведение итогов спортивного состязания в соответствии с показанными атлетом результатами. К индивидуальным спортивным дисциплинам относят такие виды спорта, как легкая атлетика, плавание, велоспорт, тяжелая атлетика, современное пятиборье, бокс, теннис и т.п. Индивидуальные виды спорта входят в программу Олимпийских игр, программу Паралимпийских игр, программу чемпионатов мира, континентов, отдельных стран и содружеств стран [1].
Результаты прогнозов в индивидуальных спортивных дисциплинах могут быть использованы в текущей подготовке спортсменов и сборных команд по видам спорта, для корректировки тренировочных программ, медальных и индивидуальных планов.
Прогнозирование в индивидуальных видах спорта заключается в решении задачи аппроксимации функции от набора параметров, где аргументами функции являются исходные параметры для прогноза, а результатом работы функции – результат прогноза. Для реализации прогноза в данной работе используется структурная модель прогнозирования на основе искусственных нейронных сетей [2, 3]. В данной работе идет речь о тех видах спорта, где результат оценивается в виде некоторого числа, как правило, действительного, выраженного в виде десятичной дроби. В частности, в данной работе рассматриваются легкоатлетические дисциплины [4].
Целями проводимых исследований являются оптимизация и повышение точности процесса прогнозирования и планирования индивидуальной спортивной подготовки путем прогнозирования спортивных результатов с использованием каскада искусственных нейронных сетей (ИНС).
Материалы и методы исследования
В предыдущих работах авторов [5] описывается прогнозирование результатов в легкоатлетических дисциплинах с использованием отдельных моделей нейронных сетей, таких как каскадная сеть, обобщенно-регрессионная сеть (GRNN), сети прямого распространения (FNN). Обучающая выборка составляется на основе имеющихся параметров, к которым могут относиться те параметры спортсмена, которые выделяют специалисты по данному виду спорта. К параметрам обучающей выборки могут относиться контрольно-тестовые показатели за период, результаты предыдущих выступлений, погодные и фармакологические параметры, векторизованные данные, основанные на мнении экспертов.
В данной работе в качестве объекта прогнозирования рассматривается результат в легкоатлетической дисциплине «Толкание ядра». В качестве обучающей выборки рассматриваются контрольно-тестовые параметры, силовые, скоростные, технические параметры, собранные по временным периодам. Для каждого временного периода составлен вектор из данных параметров. Результатом прогноза является результат атлета данной дисциплины.
Обобщенно-регрессионная нейронная сеть (GRNN) является разновидностью сетей с радиальными функциями. Данная сеть основана на непараметрической регрессии [6]. Первый слой сети полностью состоит из нейронов, функцией активации у которых является радиальная функция. Такие нейроны называют радиальными элементами. Второй слой содержит элементы, которые помогают оценить взвешенное среднее. При обучении GRNN-сетей сначала настраиваются центры базисных функций, затем с фиксированными параметрами радиальных нейронов обучается выходной слой.
Существенный недостаток сети – размерность радиального слоя, соответствующая количеству наблюдений (векторов) в обучающей выборке.
Фрагмент обучающей выборки приведен на рисунке 1. Результат прогнозирования с использованием данной выборки описан в работе [7], где структурной моделью прогнозирования является GRNN-сеть, разработанная в среде MATLAB.
Рассматривая обучающую выборку, содержащую в каждом векторе более 10 параметров, можно заметить, что параметры могут быть логически разбиты на группы. Например, контрольные результаты жима лежа, приседаний могут быть отнесены к набору силовых параметров, результаты прыжка и рывка – к скоростно-силовым, отдельные наборы составляют технические, скоростные и фармакологические параметры. В данной выборке не учитываются погодные параметры и параметры экспертов, однако потенциально данные параметры могут учитываться, но, в частности, данные экспертов необходимо векторизовать и нормализовать.
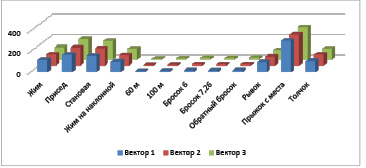
Рис. 1. Фрагмент обучающей выборки
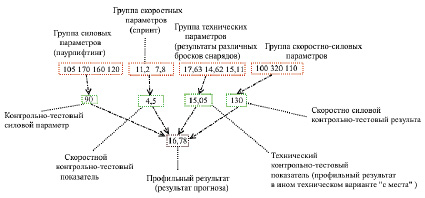
Рис. 2. Зависимости между обучающими выборками
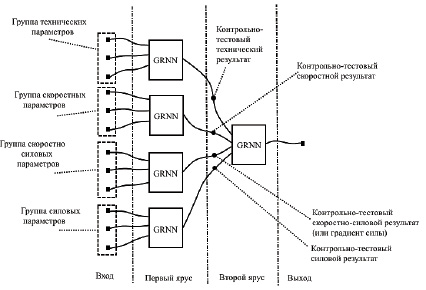
Рис. 3. Каскад GRNN-сетей
Структурно зависимости в обучающих выборках, рассматриваемые в данной работе и входящие в основу построения каскада сетей, представлены на рисунке 2. Зависимости контрольно-тестовых параметров второго яруса от групп параметров первого яруса должны определяться экспертами. Выборки (5 шт.) составляются заранее, модули каскада тоже обучаются заранее. После обучения модули включаются в каскад. Имеется возможность включения и исключения модулей при изменении структуры фрагментированной выборки, изменения количества фрагментов выборки или элементов обучающего вектора. Для обучения первого яруса каскада сетей используются четыре выборки соответственно четырем группам параметров, результирующими векторами будут отдельно выбранные контрольно-тестовые параметры. Для обучения второго яруса каскада составляется обучающая выборка из ключевых контрольно-тестовых параметров (результаты бега на 30 м, взятия штанги на грудь, толкания снаряда без разгона и жима штанги стоя), число параметров в векторе соответствует числу групп. Необходима фактическая и логическая зависимость контрольно-тестовых показателей от параметров выбранных групп, что должно определяться экспертами, в данном случае по выбранной спортивной дисциплине.
Предлагаемый в данной работе каскад приведен на рисунке 3. В качестве базовой модели для модулей каскада выбрана модель GRNN сети [8]. При поступлении данных для получения прогноза первый ярус сформирует промежуточный прогноз ключевых контрольно-тестовых параметров, которые, в свою очередь, поступят на входы второго яруса. На их основе будет сформирован прогноз профильного результата в дисциплине «Толкание ядра». Результат является вещественным числом, в виде десятичной дроби.
Для обобщенно-регрессионной сети в качестве настраиваемого параметра в данной работе рассматривается целевая ошибка, структура сети изменяется в зависимости от количества векторов в обучающей выборке, в данном случае количество векторов соответствует наблюдаемым периодам (более 300). При построении каскада, в отличие от одной сети, количество нейронов будет в пять раз больше (суммарно каскад содержит пять модулей, количество векторов в выборках будет одинаковым). Время обучения каскада превышает время обучения отдельной сети и оценивается эмпирически в разделе «Результаты экспериментов».
При необходимости данные, поступающие на первый ярус, возможно передавать напрямую на второй ярус, дополнительно к выходным параметрам первого яруса (например, если необходимо будет добавить отдельные погодные или фармакологические параметры).
Предлагаемая модель каскада смоделирована в среде MATLAB, полученные модели занимают не более 4 Мб на жестком диске.
Результаты исследования и их обсуждение
В качестве метрики оценки точности прогнозирования взята ошибка обобщения, при этом самой метрикой является средняя абсолютная ошибка (MAE), которая рассчитывается как сумма модулей разности эталона и фактического значения, поделенная на количество наблюдений. Для расчета ошибки обобщения используется тестовая выборка, по своей структуре аналогичная обучающей выборке.
Нейронная сеть и каскад обучены с использованием разработанных ранее выборок. Результаты эксперимента приведены в таблице.
Результат эксперимента
|
Целевая ошибка |
MAE (GRNN-сеть) |
MAE (Каскад) |
|
0,0001 |
0,42 |
0,37 |
|
0,001 |
0,44 |
0,37 |
|
0,01 |
0,44 |
0,37 |
|
0,1 |
0,45 |
0,37 |
|
1 |
0,63 |
0,56 |
|
10 |
1,11 |
1,78 |
|
100 |
2,74 |
2,61 |
|
1000 |
3,89 |
3,93 |
В результате эксперимента видно, что ошибка обобщения каскада незначительно меньше ошибки обобщения отдельной сети. В данном случае не применялись другие модели нейронных сетей, сеть обобщенной регрессии использована с изменением параметра целевой ошибки. Сети, используемые в каскаде, на каждом этапе эксперимента имели одинаковую целевую ошибку обучения. Целевая ошибка значением более 10 приводит к увеличению ошибки обучения и обобщения, понижению точности результата прогнозирования.
Уменьшение целевой ошибки приводит к уменьшению ошибок обучения и обобщения, увеличению точности прогнозирования. В отдельных случаях, когда такого увеличения точности будет достаточно, использование каскада имеет смысл.
Среднее время обучения отдельной сети составило 0,63 сек., среднее время обучения каскада сетей – 2,34 сек.
Заключение
Применение средств ИТ и ИИ при прогнозировании событий разного временного горизонта – перспективное направление. Корректность составляемых обучающих выборок напрямую влияет на результат прогноза. Предобработка выборки и нормализация частично решают проблему некорректной выборки при разбросе наборов параметров или отсутствии отдельных значений.
Применение каскада нейросетевых модулей позволит проводить лишь частичную нормализацию выборки там, где это необходимо, разбивая данные на фрагменты и обрабатывая отдельный фрагмент. Динамическое формирование прогнозоформирующих предикторов между ярусами позволяет использовать при прогнозировании новые параметры, ранее недоступные в выборке, при этом не изменяя выборки для первого яруса каскада.
Программный прототип системы на основе каскада нейросетевых модулей тестируется на различных обучающих выборках, результаты показывают незначительное уменьшение ошибки обобщения и коррекцию результатов прогноза при использовании каскада в правильную сторону. Часть экспериментов направлена на выявление ключевых параметров, оказывающих влияние на результат прогноза. Исключение лишних параметров выборки позволит уменьшить время обучения и структуру каскада.
Каскад обобщенно-регрессионных нейронных сетей повышает точность прогнозирования при оценке ошибки обобщения метрикой МАЕ. Необходимость повышения точности прогнозирования может быть востребована при близких итоговых результатах соревнующихся атлетов. Высокая точность имеет смысл при незначительном отличии результатов (сантиметры и десятки сантиметров в дисциплине, описываемой в статье).
При явном отличии результатов (явном преимуществе одного из соперников) малое повышение точности путем каскадирования не будет иметь смысла. Повышение времени обучения при каскадировании необходимо оценивать с точки зрения временного периода прогноза.
На основе каскада нейросетевых модулей для решения задач прогнозирования разрабатываются архитектура и структура системы. В данный момент при проведении экспериментов конкретная обучающая выборка формируется и структурируется специалистами, проводящими конкретный эксперимент. При разработке структуры и архитектуры системы следует учесть наличие модуля, производящего автоматический сбор и структурирование обучающих данных, а также модуля, формирующего нейросетевой каскад.
На данный момент продолжаются эксперименты в различных спортивных видах и дисциплинах. Используются различные простые модели нейронных сетей, отличающиеся по структуре обучающие выборки, различные алгоритмы обучения для отдельных модулей нейросетевого каскада. Усложнение отдельных модулей и предложенной структуры в целом с целью повышения точности прогноза приводит к увеличению времени работы системы. Эксперименты показывают, что систему в данный момент корректно использовать при среднесрочном и долгосрочном прогнозировании событий.
Библиографическая ссылка
Крутиков А.К., Клюкин В.Л., Подковырин В.Д. РЕШЕНИЕ ЗАДАЧИ ПРОГНОЗИРОВАНИЯ РЕЗУЛЬТАТОВ ИНДИВИДУАЛЬНЫХ СПОРТИВНЫХ ДИСЦИПЛИН С ИСПОЛЬЗОВАНИЕМ КАСКАДА НЕЙРОННЫХ СЕТЕЙ // Научное обозрение. Технические науки. 2022. № 3. С. 10-14;URL: https://science-engineering.ru/ru/article/view?id=1393 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/srts.1393


 science-review.ru
science-review.ru