Всемирная летняя Универсиада – международные и национальные спортивные соревнования среди студентов, проводимые Международной федерацией университетского спорта (FISU). Всемирная Универсиада проводится раз в два года. На предстоящих состязаниях XXXI Летней Универсиады 2022 (2021) будет представлено 18 видов спорта [1], разыграно 268 комплектов наград. Сборная РФ (ранее СССР) принимает участие в Универсиадах с начала их проведения в 1959 г.
Выступление национальных студенческих команд оценивается аналогично выступлениям национальных команд на международных мультиспортивных мероприятиях, основной мерой такой оценки является место в неофициальном командном зачете (НКЗ). Место оценивается по основной версии – согласно количеству золотых медалей. Согласно второй распространенной версии НКЗ оценивается по общему количеству медалей вне зависимости от их достоинства. Подготовкой национальной сборной в течение двух лет занимается Российский спортивный студенческий союз (РССС «Буревестник») [2]. Результаты выступления оцениваются представителями РССС, студенческих спортивных лиг и объединений. Информация широко тиражируется в СМИ. Стоит отметить что предстоящие игры Всемирной Универсиады (ВУ) были перенесены на один год, с 2021 г. на 2022 г., по причине пандемии COVID-19. Цикл подготовки команд был продлен, привычные подготовительные мероприятия перенесены или отменены. Результат НКЗ ВУ будет оцениваться специалистами национальных федераций по видам спорта и представителями РССС.
Медальный план оценивается и ставится перед студенческой сборной представителями РССС. Осуществление планирования медального плана требует работы экспертов, анализа динамики выступлений на предварительных турнирах, анализа ряда факторов, влияющих на состояние команды и отдельных спортсменов. Анализ факторов предполагает постоянную обработку данных с использованием как мнений экспертных групп [3], так и инструментов ИТ-технологий, включая направления искусственного интеллекта (ИИ) [4].
Среди таких средств можно выделить экспертные системы на основе логического вывода [5], технологии обработки больших данных, аппарат математической статистики, а также искусственные нейронные сети (ИНС), являющиеся распространенным средством прогнозирования [6].
Авторы данной работы неоднократно производили прогноз аналогичных спортивных событий, в том числе Всемирной зимней Универсиады 2019 [7] с использованием отдельных моделей ИНС. Среди используемых моделей рассматривались сети с радиальными функциями, каскадные сети прямого распространения, линейные нейронные сети и нейронные сети векторного квантования сигналов. Эксперименты проводились в том числе с использованием различных вариаций двухъярусного каскада нейросетевых модулей [8]. Одной из проблем является невозможность учета в выборке набора параметров, результаты которых прогнозируются в тот же период времени и влияют на основной результат прогноза. При добавлении таких параметров в выборку структура выборки изменяется, а следовательно, изменяется структура некоторых моделей ИНС, появляется необходимость переобучения сетей.
Авторами данной работы для решения этой проблемы применяется многоярусный каскад нейросетевых модулей, где промежуточные результаты, оказывающие влияние на результат прогнозирования, генерируются динамически, между ярусами каскада.
Объектом прогнозирования в данной статье является выступление сборной команды РФ на XXXI Летней Универсиаде 2022.
Целью проводимых исследований являются прогнозирование результатов НКЗ с использованием многоярусного каскада нейросетевых модулей, а также оптимизация и повышение точности процесса планирования спортивной подготовки студенческих сборных команд, на основе результатов прогноза.
Материалы и методы исследования
В работе [8] описывается построение двухъярусного каскада для прогнозирования результатов крупного мультиспортивного события. На первом ярусе каждый нейросетевой модуль производит промежуточный результат прогноза, с использованием отдельной модели нейронной сети, при этом каждый из модулей принимает одну логически разделенную группу параметров (условно социальную или условно спортивную), выраженную десятичными числами. Проведенные с двухъярусным каскадом эксперименты показали приближение значений к верным результатам, с использованием каскада однотипных сетей, по сравнению с одной ИНС той же модели.
Обучающая выборка фрагментируется в соответствии с логическими взаимосвязями данных, данные могут дублироваться или отличаться полностью, в зависимости от логического назначения фрагмента выборки.
На первом этапе произведены эксперименты с отдельными моделями нейронных сетей. В данном случае использованы нейронные сети с радиальными функциями – обобщенно-регрессионная нейронная сеть (GRNN) и радиально-базисная нейронная сеть (RBF).
Для обучения данных сетей формируется обучающая выборка, включающая в себя результаты выступления сборных команд РФ начиная с 1992 г. (подготовка к Универсиаде 1993). Выборка содержит социальные и спортивные параметры, которые влияют на итоговый результат прогноза. Для формирования выборки использован тот же принцип, что и в работе [8], а также [9]. Выборка содержит данные о количестве делегации сборной команды на играх, результатах выступления команд на предстоящих играм турнирах, фактор «родных стен», количестве жителей, ВВП на душу населения и т.д.
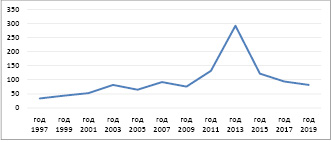
Рис. 1. Фрагмент результирующего вектора
Результирующий вектор содержит либо место в НКЗ по золотым медалям, либо общее место в НКЗ, либо отдельные результаты по общему количеству медалей, золоту или серебру. Бронзовые медали не учитываются, т.к. в НКЗ (по золоту) количество бронзовых медалей учитывается в последнюю очередь, при редком случае полного совпадения комбинации золото-серебро. Фрагмент результирующего вектора приведен на рис. 1.
В рабочем пространстве MATLAB с данными моделями нейронных сетей произведены эксперименты, результаты описываются в следующем разделе.
Часть результатов, полученных в ходе прогнозирования, могут оказывать влияние на основной прогнозируемый параметр (место сборной команды в общем зачете по общему количеству медалей или по количеству золотых медалей). В частности, речь идет о прогнозных значениях количества золотых, серебряных медалей и общего количества наград всех достоинств. При добавлении вновь полученных прогнозных значений в выборку необходимо перестроить структуру выборки, а с учетом выбранных моделей сетей при переобучении будет перестроена вся структура сети. В ряде программных и аппаратных реализаций, изменение структуры в ходе прогнозирования может быть недоступным и невозможным. В текущем эксперименте для отдельных моделей в обучающую выборку не включаются значения количества наград.
При применении каскада параметры, которые ранее не включались в выборку, формируются динамически в процессе прогнозирования, передаются между модулями каскада с одного яруса на другой. Данные значения являются промежуточными прогнозными результатами и одновременно прогнозоформирующими предикторами для модулей последующих ярусов. При обучении каскада каждый модуль обучается отдельно и включается в каскад после завершения процесса обучения.
Обучающая выборка фрагментируется следующим образом, на первом ярусе два блока параметров – социальные и спортивные, описанные ранее, в выборке, используемой для обучения отдельных моделей сетей. Во втором блоке параметров, для второго яруса, прогнозоформирующие значения количества золотых и серебряных медалей, одновременно являющиеся промежуточными прогнозными значениями для конкретного эксперимента. Третий ярус содержит третий блок прогнозоформирующих параметров, от которого зависит итоговый результат.
Структура обучающей выборки приведена на рис. 2.
Структура каскада нейросетевых модулей строится исходя из структуры фрагментированной обучающей выборки. Структура выборки приведена на рис. 3.
Авторами были спроектированы и реализованы в рабочем пространстве среды MATLAB несколько конфигураций каскада. Полученные программные модели занимают не более 8 Мбайт на жестком диске.
Результаты исследования и их обсуждение
Эксперименты проводились на модели системы спортивного прогнозирования, имеющей трехъярусную структуру, реализованную в среде MATLAB с использованием пакета Neural Network Toolbox. Нейронные сети RBF и GRNN были обучены с использованием рассмотренных в предыдущем разделе выборок. Результаты RBF-сети представлены относительно параметра сглаживания (SPREAD), результаты GRNN-сети представлены относительно значений целевой ошибки обучения (табл. 1).
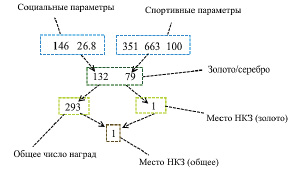
Рис. 2. Структура обучающей выборки
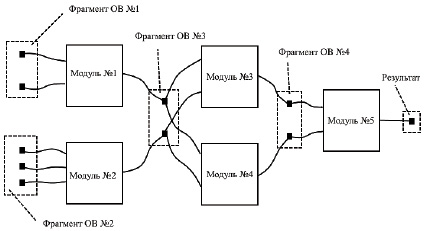
Рис. 3. Структура каскада нейросетевых блоков
Для нейронной сети с радиально-базисными функциями минимальная MSE для обучения получена при значении параметра SPREAD = 0.003.
При увеличении параметра более 3, MSE возрастает. Для обобщенно-регрессионной нейронной сети при увеличении параметра целевой ошибки более 10, MSE обучения начинает возрастать, результат прогноза при этом искажаются. Модуль на базе RBF показывает сомнительный результат – 1 место с 34 медалями, 10 из которых золотые, что маловероятно в условиях летней Универсиады.
Предлагается использование шести вариантов конфигурации каскада нейросетевых модулей. Отличие в предложенных конфигурациях заключается в расположении конкретных моделей ИНС в модулях определенных ярусов (рис. 4).
Параметры сглаживания SPREAD и целевой ошибки GOAL, соответственно в радиально-базисной сети [10] и обобщенно-регрессионной сети [11], используются равные 0.003 и 0.001 соответственно. Результаты эксперимента приведены в табл. 2.
В ходе эксперимента значение параметров не изменяется.
Таблица 1
Результат работы отдельных сетей
|
RBF-сеть |
|||
|
SPREAD |
Результат прогноза (место по золоту / общее место) |
Результат прогноза (общее число медалей) |
Результат прогноза (золото/серебро) |
|
0.000003 |
1 |
34 |
10/14 |
|
0.00003 |
1 |
34 |
10/14 |
|
0.0003 |
1 |
34 |
10/14 |
|
0.003 |
1 |
34 |
10/14 |
|
0.03 |
1 |
34 |
10/14 |
|
0.3 |
1/1 |
34 |
10/14 |
|
GRNN-сеть |
|||
|
Целевая ошибка |
Результат прогноза (место по золоту / общее место) |
Результат прогноза (общее число медалей) |
Результат прогноза (золото/серебро) |
|
0.001 |
1/2 |
122 |
35/39 |
|
0.01 |
1/2 |
122 |
35/39 |
|
0.1 |
1/2 |
122 |
35/39 |
|
1 |
1/2 |
122 |
35/39 |
|
2 |
1/2 |
122 |
35/39 |
|
50 |
1/1.23 |
117.26 |
30.26/31.11 |
|
100 |
0.92/1.42 |
114.92 |
29.37/29.73 |
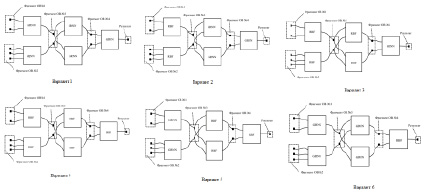
Рис. 4. Варианты конфигураций каскада
Вариант 5, очевидно, некорректно работает, следовательно, логический выбор распределения предикторов следует изменить. Варианты 2–4 демонстрируют маловероятные промежуточные данные. С точки зрения получения корректного прогноза стоит оценивать варианты 1 и 6. Точность прогноза возможно оценить после фактического завершения события. Время обучения увеличивается в среднем на 1,55 с, поскольку модули в данном эксперименте обучаются одновременно. Фактическая работа каскада не превышает 6 с, что почти в 3,6 раза больше, чем работа отдельной обобщенно-регрессионной сети. В условиях данной задачи прогнозирования данное время не является существенным.
Таблица 2
Прогноз выступления сборной РФ
|
Каскад |
Результат прогноза (место НКЗ общее) |
Промежуточный результат прогноза (место НКЗ золото) |
Промежуточный результат прогноза (золото/серебро) |
Промежуточный результат прогноза (общее количество медалей) |
|
Вариант 1 |
2 |
1 |
35/24 |
76 |
|
Вариант 2 |
2 |
4 |
10/1.34 |
34 |
|
Вариант 3 |
2 |
0.99 |
10/1.34 |
35 |
|
Вариант 4 |
0.99 |
0.99 |
10/1.34 |
35 |
|
Вариант 5 |
0.99 |
0.99 |
35/24 |
35 |
|
Вариант 6 |
0.99 |
1 |
35/24 |
76 |
Заключение
Использование информационных технологий, в частности технологий на основе нейронных сетей, при решении задач прогнозирования перспективно и широко применяемо.
По сравнению с ошибками обобщения «простых» моделей нейронных сетей (например, GRNN-сетей) ошибка обобщения при использовании каскада уменьшается, следовательно, повышается точность прогнозирования. Полученная разница во времени в задачах с долгосрочным и сверхдолгосрочным периодом прогнозирования не имеет большого практического значения.
Конечно, и время обучения каскада из нескольких нейросетевых модулей будет больше времени обучения отдельной сети. Но обычно данный этап не включается в общее время функционирования системы. Кроме того, обучение модулей каскада можно осуществлять не только последовательно, но и параллельно. Переобучение всего каскада осуществляется только при изменении структуры обучающей выборки. Переобучение отдельных модулей потребуется при добавлении в обучающую выборку новых наборов данных. При параллельном обучении время будет определяться подготовкой к работе самого «долгообучаемого» модуля.
Определение ключевых предикторов в представленном варианте специализированного модуля прогнозирования используется при оценке предельной ошибки обобщения (точности прогнозирования) самим пользователем. Он в ручном режиме может исключить некоторые параметры выборки, несущественно влияющие на изменение ошибки. В дальнейшем реализация алгоритма определения ключевых предикторов будет автоматизирована с учётом определения предельной ошибки самой системой.
Библиографическая ссылка
Крутиков А.К., Страбыкин Д.А., Подковырин В.Д. КАСКАДИРОВАНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ РЕЗУЛЬТАТОВ ВСЕМИРНОЙ УНИВЕРСИАДЫ 2021 (2022) // Научное обозрение. Технические науки. 2022. № 4. С. 11-16;URL: https://science-engineering.ru/ru/article/view?id=1403 (дата обращения: 07.01.2026).
DOI: https://doi.org/10.17513/srts.1403


 science-review.ru
science-review.ru