Расчет магнитного поля, создаваемого подвижными зарядами и токами различной конфигурации элементов, является одной из важных прикладных задач физики [1] из-за многочисленного применения в научных исследованиях, физике, технике различного направления [2, 3]. Основным требованием к конструкциям катушек, генерирующих постоянное магнитное поле, является обеспечение максимальной пространственной области однородности поля [4–6]. Для решения этой задачи предложено множество конструкций [7–9]. Виток Ампера (рис. 1–1) является простейшей конструкцией, порождающей однородное магнитное поле. Наиболее часто для генерации однородного магнитного поля используют катушки Гельмгольца, которые состоят из двух соосных витков тока одного радиуса (рис. 1–2). Установлено, что максимальный объем однородности магнитного поля достигается, когда расстояние между катушками приблизительно равно радиусу катушки.
Катушки Гельмгольца являются основным конструктивным элементом для множества систем, предназначенным для генерации однородного магнитного поля: катушек Бакера (3), катушек МакКихана (4), катушек Браунбека (5) и бипланарных катушек Моргана (6). Аналитическое исследование ограничивается расчетом ограниченного количества моделей [10–12] и проводится обычно численными методами [13–15], что затрудняет исследование физических свойств конкретных структур.
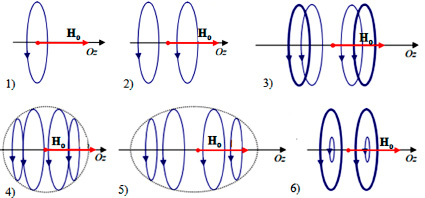
Рис. 1. Катушки для создания магнитного поля (1 – виток Ампера, 2 – катушка Гельмгольца, 3 – катушки Бэкера, 4 – катушки МакКихана, 5 – Катушки Браунбека, 6 – бипланарные катушки Моргана)
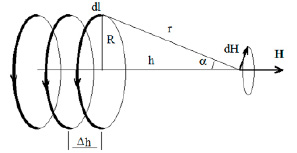
Рис. 2. Исследуемая структура
Целью исследования явилось получение аналитических соотношений для расчета напряженности магнитного поля, создаваемого системой конечного числа кольцевых токов; анализ однородности магнитного поля по оси структуры в зависимости от конфигурации системы для создания магнитных систем (формирующих локальные области с высокой однородностью магнитного поля, необходимые в различных областях измерительной [2–4] и функциональной техники [7, 8]).
Материалы и методы исследования
Исследуется однородность магнитного поля на оси нескольких систем кольцевых токов (рис. 2). Используется закон Био – Савара – Лапласа [1, 2] для нахождения магнитного поля dH , создаваемого элементом тока dl (рис. 2) на оси кругового тока на расстоянии r от центра контура:
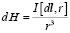 ,
,
где I – ток, r – расстояние до точки наблюдения. Векторы dH перпендикулярны плоскостям, проходящим через элемент тока dl и точку наблюдения, в которой ищется поле. Вместе они образуют конус, результирующий вектор направлен вдоль оси контура. Каждый из векторов dH вносит в результирующий вектор вклад dH\\ по модулю равный
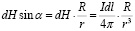 .
.
Тогда на оси кольцевого тока магнитное поле направлено перпендикулярно плоскости кольца и определяется после интегрирования по контуру проводника [2] соотношением
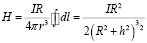 , (1)
, (1)
R – радиус кольца тока, h – расстояние от точки наблюдения на оси кольца до центра кольца.
Распределение поля по оси, перпендикулярной кольцевому току и проходящей через центр кольца, показано на рис. 3. Для одного кольцевого тока (кривая 1) распределение поля характеризуется его существенной неоднородностью. Использование нескольких соосных круговых токов позволяет регулировать распределение поля вдоль оси в широких пределах. Если соосно расположено N (дискретное количество) кольцевых токов в общем случае с разными параметрами (токами Ii , радиусами Ri, расположенными на расстояниях hi от точки наблюдения) магнитное поле определяется суперпозицией полей отдельных колец с, в общем случае, различными токами:
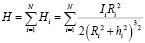 . (2)
. (2)
Результаты исследования и их обсуждение
Известно, что для создания локальных в пространстве участков однородного магнитного поля обычно используется магнитная система в виде соленоида – катушки в виде цилиндра постоянного радиуса с достаточно большим числом равномерно намотанных витков проводника, через которые пропускается ток. Это достаточно громоздкая, тяжелая и дорогостоящая конструкция (во многом из-за того, что для достижения нужных параметров часто используется медный провод, достаточно тяжелый и дорогой). Численный анализ соотношения (2) показывает, что высокая равномерность магнитного поля на оси системы колец с токами может быть обеспечена существенно меньшим по сравнению с соленоидом числом кольцевых токов, что позволяет в конечном итоге существенно снизить вес и стоимость магнитной системы.
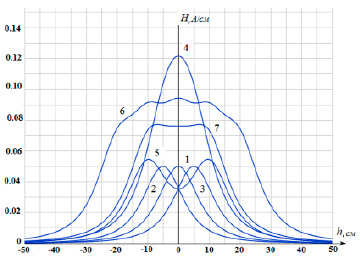
Рис. 3. Распределение поля по оси соосно расположенных тонких колец с одинаковым током и одинаковыми радиусами колец (R =10 см, ?h = 5, 10 см, 1 – распределение поля одиночного кольца с током, просматривается существенная неоднородность поля вдоль оси, 2 – распределение поля каждого из трех соосных колец, расположенных на расстоянии 5 см друг от друга, и их суммарное поле (кривая 4) также достаточно неоднородное вдоль оси структуры, 5 – поле двух колец с током, расположенных на ?h = 20 см друг от друга, 6 – поле пяти колец, расположенных по оси структуры с шагом 10 см, 7 – поле трех колец, расположенных с шагом 10 см и параметрами R3 = R1 = 10 см, R2 = 12 см, ?h = 10 см)
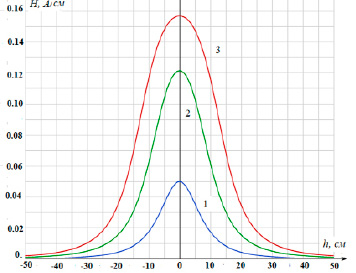
Рис. 4. Изменение поля по оси системы в зависимости от числа кольцевых витков с током (1 – один виток, 2 – три витка, 3 – пять витков)
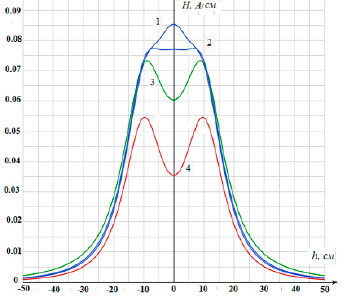
Рис. 5. Изменение структуры при изменении конфигурации системы, расстояние между соседними кольцами одинаково h =10 см (1 – три кольца одинакового радиуса 10 см, 2 – два крайних кольца того же радиуса, среднее кольцо имеет радиус 12 см, 3 – среднее кольцо имеет радиус 20 см, 4 – два кольца, расположенные на расстоянии 20 см друг от друга, среднее кольцо отсутствует)
На рис. 3 показано распределение поля для нескольких комбинаций кольцевых токов (величина тока выбиралась во всех случаях одинаковой).
Очевидно, что однородное поле может быть получено уже при использовании трех витков тока (катушка Максвелла) при изменении диаметра центрального кольца стоком (рис. 4 (кривая 7) R3 = R1 =10 см, R2 =12 см, ?h =10 см). Конструкция катушек Гельмгольца (кривая 5) также дает более высокую неоднородность магнитного поля вдоль оси системы, которая может быть уменьшена сближением колец с током и тем самым существенным уменьшением области однородного магнитного поля.
Зависимость распределения поля по оси системы соосных колец с током от числа колец показана на рис. 4 и показывает, что с ростом числа колец неоднородность поля сохраняет свой характер, хотя на расстоянии ~10 см уменьшается от 20 % (один виток с током) до 3 % (пять витков с током, расположенных с шагом 5 см). Влияние изменения радиуса центральных витков при неизменных концевых витках на структуру поля показано на рис. 5.
Кривая 1 соответствует конфигурации, когда система состоит из трех колец тока одинакового радиуса. В этом случае неоднородность поля в центре системы на расстоянии 20 см составляет ~10 %. Увеличение диаметра среднего кольца до 12 см позволяет снизить неоднородность поля величины менее 1 % (рис. 5, кривая 2). Дальнейшее увеличение радиуса среднего кольца увеличивает неоднородность поля (рис. 5, кривая 3 при радиусе 20 см).
Кривая 4 соответствует случаю отсутствия центрального кольца. Таким образом, введение центрального кольцевого тока позволяет существенно увеличить размеры области однородного поля. Проведенный анализ показывает, что дополнительные возможности регулировки и увеличения области однородного магнитного поля дает регулировка величины токов в токопроводящих кольцах, которую можно осуществлять с помощью специальных схем управления. Дополнительные возможности дает использование вместо дискретной системы кольцевых токов токопроводящих цилиндров с радиусом, меняющимся с высотой, анализ которых аналогичен описанному выше случаю с заменой операции суммирования (2) интегрированием по высоте цилиндрических источников поля.
Заключение
Рассмотрена задача расчета магнитного поля, возбуждаемого кольцевыми токами проводника круговой формы. Получены аналитические решения для системы N кольцевых соосно расположенных кольцевых токов различного диаметра. Показано, что высокая равномерность магнитного поля на оси системы колец с токами может быть обеспечена существенно меньшим по сравнению с соленоидом числом кольцевых токов, что позволяет в конечном итоге существенно снизить вес и стоимость магнитной системы. Эффект достигается не увеличением длины намотки витков соленоида, а регулировкой диаметра кольцевых токов.
Библиографическая ссылка
Глущенко А.Г., Глущенко А.А., Глущенко В.А. МАГНИТНОЕ ПОЛЕ СИСТЕМЫ КРУГОВЫХ ТОКОВ // Научное обозрение. Технические науки. 2023. № 1. С. 21-25;URL: https://science-engineering.ru/ru/article/view?id=1422 (дата обращения: 27.02.2026).
DOI: https://doi.org/10.17513/srts.1422


 science-review.ru
science-review.ru