Научный журнал

Научное обозрение. Технические науки

ISSN 2500-0799

ПИ №ФС77-57440

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Корбуков Г.М. 1 Мензульский С.Ю. 1

---

1 ФГБОУ ВО «Московский государственный технический университет имени Н.Э. Баумана»

В статье представлены результаты построения конечно-элементной модели двухлопастного авторотирующего несущего винта, ее валидации и расчета на собственные колебания. Описан проведенный эксперимент по определению жесткостных характеристик прототипа несущего винта, указаны граничные условия и нагружения, представлены полученные значения прогиба и деформаций лопасти несущего винта. Дано подробное описание процесса построения и структуры полученной конечно-элементной модели. Проведен статический анализ модели несущего винта с целью определения жесткостных характеристик. Выполнена валидация модели, при которой осуществлялся подбор параметров свойств материала и соединительных узлов, с целью сравнения расчетных и экспериментальных данных статического расчета. При выполнении валидации получены погрешности значений деформаций лопасти несущего винта между расчетной моделью и экспериментом, из которых сделаны выводы о сходимости валидированной конечно-элементной модели. Выполнен расчет конечно-элементной модели несущего винта на собственные колебания, определены собственные частоты и формы колебаний конечно-элементной модели несущего винта. Определена минимальная допустимая частота вращения двухлопастного авторотирующего несущего винта на этапе предраскрутки. Получен вывод о дальнейшем использовании модели в последующих испытаниях и расчетах.

Статья в формате PDF

1247 KB

авторотирующий несущий винт

конечно-элементная модель

валидация

собственные частоты

собственные формы

1. Миль М.Л., Некрасов А.В., Браверман А.С., Гродко Л.Н., Лейканд М.А. Вертолеты. Расчет и проектирование. М.: Машиностроение, 1967. Кн. 2. 424 с.

2. Моисеев В.С., Моисеева Л.Т. Методы предварительного проектирования беспилотных вертолетов. Казань: РИЦ «Школа», 2022. 211 с.

3. Аринчев С.В. Теория колебаний неконсервативных систем: учеб. пособие для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 459 с.

4. Дудковски Д., Джафари С., Капитаняк Т. Скрытые факторы в динамических системах // Доклады по физике. 2016. Т. 637. С. 1–50.

5. Киселев И.А., Мензульский С.Ю., Елисеев П.С., Цветков О.И. Расчетно-экспериментальные исследования прочностных характеристик авторотирующего несущего винта мотовездехода // Транспортное, горное и строительное машиностроение: наука и производство. 2024. № 25. С. 60–66.

6. Бидерман В.Л. Теория механических колебаний: учебник для вузов. М.: URSS: Ленанд, 2017. 405 с.

7. Харитонов С.А., Ципилев А.А. Динамика механических систем: учеб. пособие. М.: Изд-во МГТУ им. Н.Э. Баумана, 2017. 198 с.

8. Богоявленский А.А. Анализ процедур обеспечения достоверности средств и методов измерения вибрации в процессах поддержания летной годности воздушных судов // Научный вестник МГТУ ГА. 2017. № 1. С. 78–87.

9. Chechurin S., Chechurin L. Physical Fundamentals of Oscillation Theory: Frequency Analysis of Periodic Motion Stability. Springer International Publishing, 2018. 220 р.

С 2020 г. МГТУ им. Н.Э. Баумана проводятся работы по созданию наземно-воздушных вездеходов (НВВ), способных перемещаться по земле и в воздухе. В процессе предпроектного анализа НВВ было принято решение об использовании аэродинамической схемы автожира и, соответственно, установке на прототип авторотирующего несущего винта (НВ) с общим горизонтальным шарниром (ГШ). Динамика конструкции несущего винта всегда являлась одной из основных проблем винтокрылых аппаратов [1, с. 15–18; 2, с. 180–182]. В подобных задачах отправной точкой является определение собственных частот колебания конструкции и построение валидированной конечно-элементной модели для дальнейших расчетных исследований [3, с. 82–88; 4].

В рамках инициативной научно-исследовательской работы в МГТУ им. Н.Э. Баумана был изготовлен специализированный экспериментальный стенд на базе мотовездехода BRP Outlander 6x6 с установленным авторотирующим несущим винтом от автожира «Казачок».

Помимо ходовых испытаний специализированный стенд был использован для экспериментальных исследований напряженно-деформированного состояния несущего винта мотовездехода (рис. 1). Жесткостные испытания заключались в тензометрировании лопасти и комлевой части НВ, нагружении концевой хорды лопасти грузом весом 99,47 Н и измерении возникающих вдоль размаха лопасти линейных деформаций.

Три тензодатчика были установлены на нижнюю поверхность лопасти несущего винта (рис. 2). Лопасть, не используемая для установки тензодатчиков, была зафиксирована с помощью крепежной стропы. Нагружение было выполнено ступенями приложения нагрузки.

Результаты жесткостных испытаний, осредненные по трем измерениям, представлены в табл. 1.

Более подробно процесс проведения и результаты испытаний наглядно представлены в статье [5].

Построение модели

Построение конечно-элементной модели авторотирущего несущего винта должно выполняться в соответствии с упруго-массовыми свойствами его конструкции [6, с. 379–381; 7, 82–83].

Авторотирующий несущий винт состоит из следующих элементов: несущая балка (из трех частей: одной центральной и двух боковых), центральный болт, 2 несущих болта, 2 лопасти, 2 длинных и 2 коротких противофлаттерных стержня.

Рис. 1. Жесткостные испытания несущего винта специализированного стенда

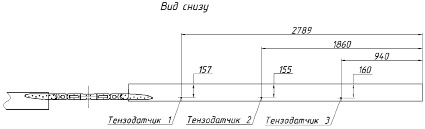
Рис. 2. Схема установки тензодатчиков

Таблица 1

Результаты прогибов и деформаций несущего винта специализированного стенда

Несущая балка несущего винта моделируется трехмерными тетраэдрическими конечными элементами первого порядка. Каждая из двух боковых частей балки соединена с центральной с помощью несущего болта.

Несущий болт моделируется как bush-элемент и соединен с краями отверстий центральной и боковой частей балки через MPC-элементы. Bush-элемент необходим для задания жесткости соединения между центральной и боковой частями балки и угла шага лопасти.

Центральный болт установлен в центральном отверстии центральной части балки, моделируется как bush-элемент, соединенный с краями отверстия в центральной балке через MPC-элементы.

Лопасть моделируется трехмерными тетра-призматическими и гексаэдрическими конечными элементами первого порядка. Для создания использовалась плоская геометрическая модель сечения лопасти. На ней создавалась сетка из двумерных треугольных и квадратных конечных элементов первого порядка, а затем эта сетка вытягивалась по нормали к плоскости сечения, образуя трехмерную сетку. Каждая лопасть крепится к боковой части несущей балки с помощью 14-и MPC-элементов (по 7 на верхней и нижней сторонах лопасти), соединенных с отверстиями в балке.

Противофлаттерные стержни моделируются трехмерными тетра-призматическими и гексаэдрическими конечными элементами первого порядка. Для создания использовались узлы конечно-элементной сетки лопасти и плоская геометрическая модель сечения стержней. С их использованием создавалась сетка из двумерных треугольных и квадратных конечных элементов первого порядка, а затем эта сетка вытягивалась по нормали к плоскости сечения, образуя трехмерную сетку. Каждый стержень (длинный и короткий) соединен с лопастью непосредственно через узлы сетки.

Таким образом, для расчета динамики конструкции несущего винта была создана конечно-элементная модель размерностью 265 тысяч узлов.

Валидация модели

Решением задачи валидации модели несущего винта является подбор свойств материалов и соединительных узлов модели для статического анализа, при котором будут получены значения деформаций и перемещений, соответствующие полученным в результате эксперимента [8].

В качестве основного материала всей конструкции принимается алюминий. Исходные параметры: модуль упругости 1 рода 71 ГПа, коэффициент Пуассона 0,3, плотность материала 2700 кг/м3.

Для согласования результатов статического анализа полученной модели с результатами эксперимента к ней приложены следующие граничные условия. На центральный болт наложены ограничение перемещений по всем осям и ограничение вращения вокруг вертикальной и продольной осей. На одной лопасти наложено ограничение перемещения узлов нижней дальней кромки по вертикальной оси. На конце другой лопасти приложена распределенная по узлам нагрузка с суммарным значением 99,47 Н вдоль вертикальной оси (рис. 3).

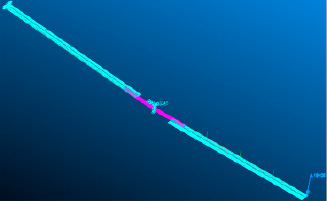
Рис. 3. Конечно-элементная модель, граничные условия и схема нагружения конечно-элементной модели

Таблица 2

Расчетные величины прогибов и линейных деформаций несущего винта специализированного стенда

При проведении статического анализа значения деформации конструкции определялись в точке размещения тензодатчика № 1 (на расстоянии 2789 мм от дальнего конца и 157 мм от задней части лопасти). Для получения значений, совпадающих со значениями из эксперимента, необходимо менять значение модуля упругости материала. В результате изменения этих свойств были получены требуемые значения деформации, данные приведены в табл. 2.

Значения перемещения дальнего конца лопасти регулируются значениями упругости несущих болтов и значением модуля упругости материала. Поскольку свойства материала были заданы раннее при измерении деформации, для получения значений перемещений, совпадающих со значениями из эксперимента, необходимо менять значения упругости несущих болтов (то есть bush-элементов).

В процессе валидации конечно-элементной модели было обнаружено, что в зависимости от вариации параметров материалов, модель показывает высокую сходимость с экспериментом либо по величинам деформации, либо по значению прогиба кончика лопасти. Это связано с тем, что при высоких значениях прогиба концевой хорды лопасти конструкция становится геометрически нелинейной. Так как собственные колебания – это малые колебания вокруг положения статического равновесия, рационально [9, с. 44] проводить валидацию по значениям экспериментально измеренных деформаций конструкции.

Расчет погрешности конечно-элементной модели выполнен по формуле

,

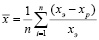где 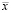– значение среднего отклонения, хэ – экспериментально измеренная линейная деформация, хр – расчетная линейная деформация, n – количество валидируемых точек. По результатам расчетов 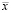составляет 5,4 %.

По результатам выполнения задачи была получена валидированная модель несущего винта. Данная модель будет использована для расчетных исследований параметров роторной динамики и динамических аэроупругих характеристик авторотирующего несущего винта.

На рис. 4 представлено деформированное состояние конечно-элементной модели.

Результаты расчета собственных колебаний несущего винта

Результаты расчетов собственных колебаний несущего винта на горизонтальном шарнире приведены в табл. 3.

Для примера на рис. 5 приведена пятая форма собственных колебаний несущего винта.

Рис. 4. Результаты статического анализа конечно-элементной модели

Таблица 3

Результаты модального анализа несущего винта на горизонтальном шарнире

Рис. 5. Пятая форма колебаний несущего винта

Выводы

1. Разработана конечно-элементная модель двухлопастного авторотирующего несущего винта. Модель провалидирована по результатам жесткостных испытаний. Получена сходимость 94,6 % по величинам экспериментальных и расчетных значений деформации конструкции.

2. Проведен расчет собственных частот и форм колебаний двухлопастного авторотирующего несущего винта. Показано, что система предраскрутки несущего винта должна обеспечивать частоту вращения НВ не менее 165 об/мин.

3. Разработанная конечно-элементная модель будет использована для расчетных исследований параметров роторной динамики и динамических аэроупругих характеристик авторотирующего несущего винта.

Библиографическая ссылка