science-review.ru
Введение
Линейная регрессия является фундаментальным методом в машинном обучении, широко используемым для предсказания непрерывных результатов [1, 2]. Однако, когда данные большой размерности, линейные регрессионные модели могут стать склонными к переобучению, что приводит к плохой обобщающей способности [3 с. 57]. При прогнозировании цен на бриллианты необходимо учитывать множество независимых друг от друга признаков, таких как вес, цвет, качество огранки, прозрачность и пр. В случае применения модели полиномиальной регрессии количество признаков вырастает кратно степени полинома и вследствие этого модель начинает излишне хорошо ложиться на тренировочный набор данных, что, естественно, приводит к высокому качеству на обучающих данных [4]. Но при этом страдает ее предсказательная способность на тренировочном наборе, то есть модель начинает подстраиваться под данные вместо того, чтобы искать зависимости, это явление и называется переобучением [3, с. 58].
Для улучшения интерпретируемости модели авторы используют такие методы, как L1 и L2 регуляризация [5], в которых для уменьшения переобучения по сути добавляется штрафной член к функции потерь, который препятствует большим весам, способствуя более простым моделям [6], которые лучше обобщаются на новые данные [4].
Целью исследования является реализация алгоритмов L1 и L2 регуляризации и их применение для построения полиномиальной регрессионной модели, позволяющей спрогнозировать цену на бриллианты, в зависимости от их веса, цвета, качества огранки, прозрачность и прочих признаков.
Материалы и методы исследования
Для построения модели, которая будет предсказывать цену на бриллианты, был использован набор данных с Kaggle. В качестве признаков выделяются: вес бриллианта в каратах; качество огранки (удовлетворительное, хорошее, очень хорошее, высшее, идеальное); цвет бриллианта, от J (худший) до D (лучший) [7]; чистота – мера чистоты бриллианта (I1 (худшая), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (наилучшая)); x, y, z – размеры бриллианта; глубина; ширина площадки верха алмаза относительно самой широкой точки. Для категориальных признаков, таких как качество огранки, цвет, чистота проведем перекодировку их в числовые. Пример преобразованных данных представлен на рис. 1.
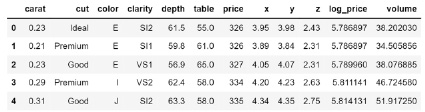
Рис. 1. Первые 4 записи в датасете
Для определения стоимости бриллиантов, в зависимости от выбранных признаков была использована модель полиномиальной регрессии [8, 9], где для аппроксимации будем искать многочлен, наилучшим образом описывающий данные. То есть входная переменная одна и находятся оптимальные коэффициенты многочлена степени k, описывающие данные из D =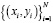 
, обозначим 
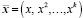, тогда отклик или моделируемую переменную можно выразить следующим образом:
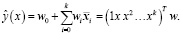(1)
В случае регуляризации L1, также называемой Лассо, в уравнение (1) добавляется дополнительное слагаемое, налагающее «штраф» за сложность модели, то есть высокие веса (ограничивая сумму абсолютных значений параметров модели |wi|):
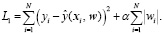(2)
Такой подход помогает решить задачу отбора признаков, так как в процессе построения модели с использованием L1 регуляризации некоторые весовые значения могут оказаться нулевыми. Это позволяет исключить признаки, которые слабо влияют на целевую переменную, и тем самым способствует упрощению модели и улучшению обобщающей способности
Для сравнения, в работе будет рассмотрена регуляризация L2, также называемая Ridge регрессией, которая добавляет к целевой функции штрафную функцию
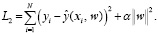(3)
В отличие от регуляризации L1, построение Ridge регрессии не приводит к обнулению ни одного из параметров модели, но также позволяет повысить устойчивость модели.
Результаты исследования и их обсуждение
Реализованные алгоритмы были протестированы на следующем примере: для обучающей выборки были заданы 60 точек (x, y), распределенных равномерно на промежутке [–5,5] × [–5,5], посчитаем значение функции в этих точках согласно уравнению (4) и добавим к результату шум, имеющий нормальное стандартное распределение.
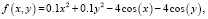
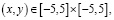(4)
На рис. 2 изображен график поверхности, описанной уравнением (4), и смоделированные значения.
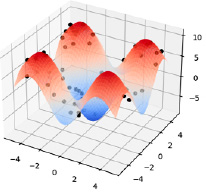
Рис. 2. График функции
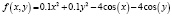
Для тестовой выборки было сгенерировано 500 значений, и в качестве базовых функций для регрессионной модели были выбрана модель третьей степени из элементов x, y, cos(x), cos(y), sin(x), sin(y).
В результате получили явно переобученную модель, поверхность проходит очень близко ко всем сгенерированным точкам, что можно видеть на рис. 3, значение среднеквадратичной ошибки (MSE) для тестового набора данных оказалось равным 1051.755.
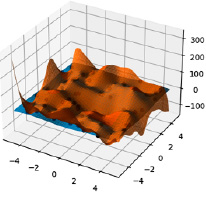
Рис. 3. Результат переобучения
При построении модели с использованием регуляризации L1 наилучшее значение MSE [10] получилось равным 0.661, при коэффициенте регуляризации равным α = 0.071.
Также для данного набора данных была построена модель с использованием L2 регуляризации, наилучшее значение среднеквадратической ошибки, равное 1.2, было получено при коэффициенте регуляризации α = 3.162.
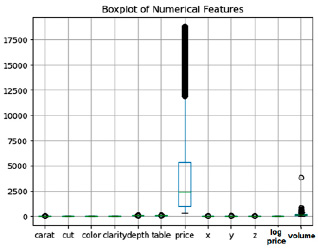
Рис. 4. Проверка на наличие шумов в данных
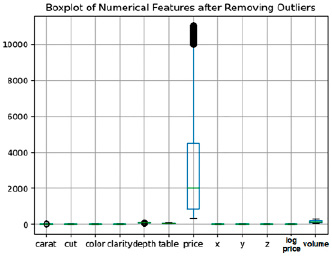
Рис. 5. Данные после очистки от шумов
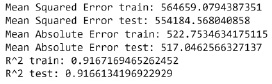
Рис. 6. Метрики для линейной модели
Можно заключить, что разработанные алгоритмы действительно позволяют строить модели с большим количеством признаков, исключая явление переобучения. Для построения модели, которая будет определять стоимость бриллиантов также была использована модель полиномиальной регрессии с использованием регуляризации, дальше будет показано ее преимущество перед моделью линейной регрессии.
В качестве первоначальной обработки очистим данные от шумов с помощью boxplot.
Как видим на рис. 4, в выборке присутствует достаточно много шумов. В результате очистки данных было удаленно 7000 записей, результат представлен на рис. 5.
Для начала рассмотрим модель простейшей линейной регрессии для прогнозирования цены на бриллианты. Исключим из выборки значения log_price – логарифм цены, так как очевидно он явным образом зависит от цены. В качестве метрик качества модели были выбраны стандартные MSE – среднеквадратичная ошибка, MAE – Средняя абсолютная ошибка, а также коэффициент детерминации R2 [10], который показывает насколько хорошо модель соответствует данным. На рис. 6 представлены значения метрик для тестовой и обучающей выборки при построении линейной модели.
Значения для тестовой и обучающей выборок получились примерно одинаковые, следовательно, переобучения в данном случае не происходит, и применять регуляризацию в данном случае не имеет смысла. Также видим, что MAE и MSE не очень показательны в данном случае, поэтому будем ориентироваться на R2, значение которого для линейной модели получилось очень неплохим, попробуем улучшить качество модели за счет использование полиномиальной модели.
Построим на данных полином 7 степени, а потом для него линейную регрессионную модель. Значение метрик качества для обучающей и тестовой выборки отображены на рис. 7 и 8.
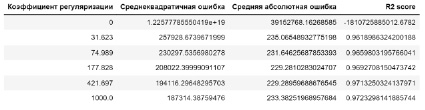
Рис. 7. Метрики для обучающей выборки
Рис. 8. Метрики для тестовой выборки
Рис. 9. Метрики при различных коэффициентах регуляризации Лассо
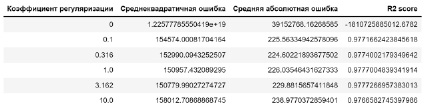
Рис. 10. Метрики при различных коэффициентах гребневой регуляризации
В данном случае получили явное переобучение, почти идеальное совпадение результата для обучающей выборки и огромная погрешность на тестовых данных. Попробуем регуляризировать полученную модель.
Применим сначала регуляризацию Лассо с различными коэффициентами, чтобы выявить лучший результат. Возьмем следующие коэффициенты регуляризации: α = [0.1,0.316,1.0,3.162,10.0]. На рис. 9 изображены значения MSE, MAE и коэффициента детерминации в зависимости от значения коэффициента регуляризации
Как видно, модель стала намного лучше работать, пропал эффект переобучения. Наилучший результат получился при α = 3.162, R2 ≈ 0.97773, что также дает преимущество перед моделью линейной регрессии (тот же вывод можно сделать, опираясь на другие метрики качества)
Применим для тех же данных регуляризацию L2 и сравним качества построенных моделей.
Возьмем следующие коэффициенты:
α = [31.623,74.989,177.828,421.697,1000.0].
Значение метрик качества модели с использование Ridge регрессии приведено на рис. 10.
Как и в предыдущем случае, можно отметить существенное улучшение качества модели по сравнению с линейной. Максимальное значение метрики R2 ≈ 0.97773 при α = 1000.
Сравнивая значения ключевых метрик при применении различных методов регуляризации, можно заключить, что серьезного различия в данном случае нет, но применение регуляризации является необходимой мерой при построении полиномиальной модели для прогнозирования цен на бриллианты.
Заключение
Как видно из приведенных исследований, при решении задачи регрессии с большим количеством признаков методы регуляризации L1 и L2, существенно улучшают как точность предсказаний, так и интерпретируемость моделей и оказывают положительное влияние на обобщаю способность. Эти методы играют ключевую роль в предотвращении переобучения, что особенно важно при работе с большими и сложными наборами данных, где модели могут чрезмерно подстраиваться под обучающие данные.
Авторами была получена робастная модель для прогнозирования стоимости бриллиантов в зависимости от веса, прозрачности, качества обработки и других признаков. Перспективные направления дальнейших исследований включают изучение и применение других методов регуляризации, таких как эластичная сеть (Elastic Net), которая комбинирует преимущества L1 и L2 регуляризации, а также более сложных подходов, например, регуляризация в байесовских методах или методов, основанных на априорных знаниях.
Библиографическая ссылка
Облакова Т.В., Григорян В.М., Зубарев К.М. ПРИМЕНЕНИЕ РЕГУЛЯРИЗАЦИИ ПРИ ПОСТРОЕНИИ ПОЛИНОМИАЛЬНЫХ РЕГРЕССИОННЫХ МОДЕЛЕЙ НА ПРИМЕРЕ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ БРИЛЛИАНТОВ // Научное обозрение. Технические науки. – 2024. – № 5. – С. 31-36;URL: https://science-engineering.ru/ru/article/view?id=1485 (дата обращения: 23.11.2024).