science-review.ru
Введение
Ионный обмен металлов занимает центральное место во множестве научных и прикладных дисциплин, таких как металлургия, электрохимические технологии и экологические проекты, направленные на устранение тяжёлых металлов из промышленных сточных вод [1–3]. Этот процесс лежит в основе методик извлечения, очистки и рафинирования металлов, а также играет критическую роль в функционировании аккумуляторных батарей. Несмотря на то что накоплен значительный практический опыт применения, дальнейшее развитие требует создания усовершенствованных математических моделей, способных учитывать широкий спектр факторов, определяющих эффективность данных реакций.
Разработка таких моделей особенно актуальна для процессов обмена ионов металлов, таких как золото и серебро, которые находят широкое применение в высокотехнологичных отраслях: электронике, медицине, а также производстве ювелирных изделий [4–6]. Эффективная математическая формализация этих процессов может существенно увеличить их экономическую целесообразность и расширить технологические горизонты. В современных исследованиях акцент делается на уточнении механизмов, идентификации ключевых переменных и оптимизации условий проведения реакций [7; 8].
Актуальность работы усиливается необходимостью повышения производительности существующих технологических процессов, уменьшения издержек и снижения экологических рисков. Однако, несмотря на значительные достижения в данной области, текущие математические модели нередко базируются на чрезмерно упрощённых предположениях, таких как равенство коэффициентов диффузии или игнорирование конвективных потоков. Эти упрощения серьёзно ограничивают применимость моделей в условиях реального производства [9–11].
Предполагается, что такая модель обеспечит возможность точного определения оптимальных характеристик процессов ионного обмена металлов. Ключевые параметры, подлежащие анализу, включают концентрацию ионов, коэффициенты диффузии, температурные условия, а также геометрические особенности системы, такие как расстояние между электродами. Предполагается, что учёт и корректировка этих факторов позволят целенаправленно управлять процессами и существенно повысить их эффективность.
Цель исследования – создание комплексной математической модели, интегрирующей уравнения, описывающие потоки ионов, плотность тока и связанные параметры.
Основными задачами исследования являются:
1. Построение математической системы, отражающей взаимосвязи между потоками ионов, плотностью тока и другими ключевыми характеристиками.
2. Аналитическое решение полученных уравнений для выявления доминирующих факторов, влияющих на результативность процесса.
3. Изучение влияния таких переменных, как концентрация ионов, геометрические размеры системы и температура, на производительность ионного обмена.
4. Оценка ограничений предложенной модели и определение направлений адаптации данной модели для использования в реальных технологических условиях.
Таким образом, данная работа не только закладывает основу для модернизации процессов ионного обмена в металлургии и экологии, но и способствует формированию более надёжных подходов к управлению и контролю таких процессов.
Материалы и методы исследования
Для проведения настоящего исследования была применена совокупность математических моделей, основанных на уравнениях Нернста – Планка. Эти уравнения, описывающие ионные потоки с учетом процессов диффузии и миграции, предоставили возможность детально моделировать основные явления, происходящие в исследуемой системе [12]. Особое внимание уделялось условиям стационарного режима, что в сочетании с отсутствием конвекции способствовало упрощению расчетов, не снижая точности анализа.
Расчет электрического потенциала в исследуемой системе был выполнен с использованием подхода, предложенного в работе [4]. Этот метод позволил установить количественные зависимости между приложенным внешним напряжением и распределением электрического поля, что сыграло ключевую роль в оценке закономерностей ионного обмена. При этом электронейтральность системы поддерживалась благодаря методике, описанной в исследовании [5], что исключило влияние побочных эффектов, таких как адсорбция, обеспечивая чистоту экспериментальных данных.
Для обеспечения стабильности концентраций ионов и корректности баланса массы применялось уравнение, рекомендованное в работе [6]. Этот подход позволил достичь высокой точности в описании динамических характеристик модели, что критически важно для проверки теоретических предсказаний.
Дополнительно в исследовании было рассмотрено влияние геометрических характеристик электродов, таких как форма и площадь поверхности, а также температурных условий. Основываясь на данных из работ [7; 8], провели анализ, выявляющий, как различные параметры электродов сказываются на эффективности ионного обмена. Более того, изучение температурных эффектов и варьирования концентрации ионов проводилось в соответствии с методологией, представленной в исследованиях [9; 10]. Сопоставление полученных данных с теоретическими моделями подтвердило обоснованность выбранных подходов и применяемых методов.
Результаты исследования и их обсуждение
Исследование позволило разработать ряд математических моделей, детально описывающих механизмы ионного обмена металлов. В основу легла система уравнений, которая включает выражения для потоков ионов (уравнение Нернста – Планка), соотношение для плотности тока и условие электронейтральности, а также взаимосвязь напряжения с электрическим полем. Чтобы упростить задачу и получить аналитическое решение, было принято несколько допущений, среди которых выделяются представление системы как эквивалентного бинарного электролита и рассмотрение стационарного режима. Анализ итоговых уравнений позволил выделить главные параметры, определяющие ход исследуемого процесса.
Полное описание процесса ионного обмена металлов представлено математической моделью, включающей следующую систему уравнений.
Уравнение Нернста – Планка
Диффузия, миграция и конвекция составляют поток ионов Ji. При отсутствии учета конвекции уравнение Нернста – Планка записывается следующим образом:
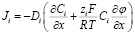, (1)
где Ji – плотность потока ионов (моль/(м²·с)), Di – коэффициент диффузии ионов (м²/с), Ci – концентрация ионов (моль/м³), x – расстояние (м), zi – заряд иона, F – постоянная Фарадея (96,485 Кл/моль), R – универсальная газовая постоянная (8.314 Дж/(моль·К)), T – абсолютная температура (К), φ – электрический потенциал (В).
Уравнение плотности тока
Общий ток i пропорционален сумме потоков всех ионов:
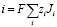. (2)
Подставляя уравнение потока ионов в уравнение плотности тока, получаем общую математическую модель.
Полная формула плотности тока
Подставляем полученное уравнение для Ji в уравнение для i:
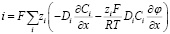(3)
Если раскрыть скобки в этом уравнении, получится следующее:
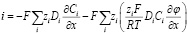(4)
Введя обозначения в уравнение, получим следующее:
– диффузионный компонент^
iдиффузия =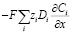 
(5)
– миграционный компонент^
iмиграция =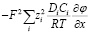 
(6)
Таким образом, общая плотность тока будет следующей:
i = iдиффузия + iмиграция (7)
Условие электронейтральности
В ионном растворе общий заряд должен быть электронейтральным:
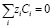(8)
Уравнение баланса массы (стационарное состояние)
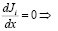Ji = констатнта (9)
Связь напряжения и электрического поля
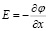, U = φ(0) – φ(L) (10)
Авторская цель – аналитически решить эту систему уравнений и найти функции Сi(х) и φ(х).
Для аналитического решения системы уравнений примем следующие упрощающие предположения:
1. Эквивалентный бинарный электролит:
• Ионы: катион (z+) и анион (z–).
• Заряды равны по абсолютной величине:
|z+| = |z–| = z.
• Коэффициенты диффузии равны:
D+ = D– = D.
2. Электронейтральность:
zC+ – zC– = 0 ⇒ C+ = C– = C.
3. Стационарное состояние и отсутствие конвекции:
• Постоянные потоки ионов:
dJi / dx = 0.
• Конвективные потоки отсутствуют.
4. Суммарный массовый поток равен нулю:
J+ + J– = 0.
Решение уравнений
1. Уравнения потока ионов
Для катиона (z+ = +z):
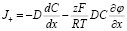(11)
Для аниона (z– = –z ):
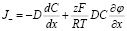(12)
2. Общее уравнение плотности тока
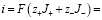
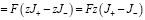(13)
3. Суммарный массовый поток равен нулю
J+ + J– = 0 ⇒ J– = –J+ (14)
4. Выражение для плотности тока
Подставляем J– = –J+ в уравнение плотности тока:
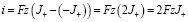(15)
Отсюда находится J+:
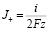(16)
5. Подстановка потока катиона в уравнение
Подставляем J+ в уравнение для J+
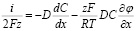(17)
Учитывая, что суммарный массовый поток равен нулю и концентрация постоянна (dC / dx = 0), уравнение упрощается:
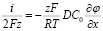(18)
6. Выражение для градиента потенциала
Решаем относительно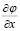 
:
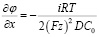(19)
Градиент потенциала является константой и не зависит от координаты x.
7. Распределение электрического потенциала
Интегрируем по x:
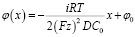, (20)
где φ0 – потенциал при x = 0.
8. Определение напряжения
Напряжение между электродами U:
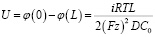(21)
9. Связь между током и напряжением
Получаем линейную зависимость:
U = Ri, (22)
где сопротивление R:
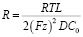(23)
Результаты
• Концентрация: C(x) = C0 – постоянная величина.
• Электрический потенциал в рассматриваемой системе может изменяться пропорционально координате x:
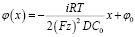(24)
• Напряжение: между током и напряжением существует линейная зависимость:
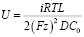(25)
Проведённый детальный анализ уравнений, описывающих процессы ионного обмена металлов, позволил выделить ключевые закономерности, существенно углубляющие понимание сложного явления. В рамках данного исследования были сформулированы и обоснованы математические модели, способные с высокой точностью описывать основные аспекты ионного обмена. Анализ показал, что на эффективность процесса существенно влияют такие параметры, как концентрация ионов, диффузионные свойства среды, геометрические характеристики электродов, включая форму и площадь, а также расстояние между ними.
Исследование продемонстрировало, что плотность электрического тока находится в линейной зависимости от приложенного напряжения. Этот факт подтверждает справедливость теоретических положений закона Ома и одновременно упрощает задачи оптимизации системы.
На основе полученных данных были сделаны следующие выводы.
1. Геометрия и площадь электродов. Увеличение площади поверхности электродов способствует снижению сопротивления системы, что, в свою очередь, приводит к повышению эффективности ионного обмена. Равномерное распределение электрического поля в значительной мере зависит от формы и конфигурации электродов. Оптимизация этих параметров открывает новые возможности для повышения производительности промышленных установок.
2. Влияние температуры. Повышение температуры электролита приводит к увеличению проводимости, что связано с возрастанием коэффициента диффузии. Однако при достижении определённых критических температур может наблюдаться дестабилизация физико-химических свойств среды, что негативно сказывается на общей эффективности системы. Это подчеркивает необходимость точного контроля температурных условий в технологических процессах.
3. Концентрация ионов и расстояние между электродами. Высокая концентрация ионов в электролите положительно влияет на проводимость, в то время как увеличение расстояния между электродами приводит к росту сопротивления, ухудшая эффективность обмена. Эти параметры являются определяющими для разработки более энергоэффективных решений без необходимости сложных модификаций оборудования.
Сформулированные модели подтвердили свою высокую прогностическую ценность при описании стационарных процессов и отсутствия конвективных эффектов. Используя уравнение Нернста – Планка и его производные, удалось получить аналитические зависимости, обеспечивающие детализированное описание поведения системы при различных условиях. Выводы исследования согласуются с результатами предыдущих работ, где значимость геометрических факторов в электролизе была подтверждена эмпирически.
Тем не менее предложенная модель имеет ограничения: не учитывает влияние конвективных потоков и предполагает равенство коэффициентов диффузии для всех ионов, что снижает применимость к более сложным системам. Для решения этих вопросов необходимы дальнейшие исследования, направленные на создание более универсальных моделей, способных учитывать нестационарные и неоднородные условия.
Результаты данной работы предоставляют широкие перспективы для улучшения существующих систем ионного обмена. Они предлагают научно обоснованный подход к выбору параметров, обеспечивая максимальную производительность с минимальными затратами. Внедрение таких моделей на практике может существенно повысить эффективность промышленных процессов, связанных с ионным обменом.
Заключение
Таким образом, разработанные математические модели предоставляют надежный инструмент для оптимизации и управления процессами ионного обмена металлов. В то же время для более точного описания реальных условий необходимо учитывать динамические изменения, такие как неравномерная концентрация и наличие конвекции. Дальнейшие исследования должны быть направлены на расширение и улучшение существующих моделей, включая применение численных методов для анализа более сложных и динамических систем, что позволит повысить точность и универсальность применения в промышленных и экологических технологиях.
Библиографическая ссылка
Сатыбалдыев А.Б. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ В ПРОЦЕССЕ ИОННОГО ОБМЕНА МЕТАЛЛОВ // Научное обозрение. Технические науки. – 2025. – № 1. – С. 5-9;URL: https://science-engineering.ru/ru/article/view?id=1491 (дата обращения: 23.02.2025).