science-review.ru
Введение
Фильтрационный поток через насыпную (грунтовую) плотину является одним из важнейших показателей надежности и экономической эффективности гидротехнического сооружения (ГТС). При проектировании или эксплуатации (реконструкции) ГТС необходимо обладать численными данными о силах механического воздействия фильтрационного потока на объект гидротехнического назначения [1, с. 17], положении депрессионной кривой в профиле плотины, химическом составе грунтов и воды и др. [2, с. 33]. Решение комплексных задач по определению показателей фильтрации через тело плотины сводится к использованию гидромеханических, численных, аналоговых и гидравлических методов [3, с. 374].
На сегодняшний день такие решения получены для случаев изотропных фильтрационных свойств грунтов, как наиболее идеальных типов грунтов, для которых имеется понятное и точное математическое описание [3, с. 54; 4, с. 112]. В практике расчетов фильтрационных показателей работы грунтовых плотин зачастую приходится иметь дело с анизотропностью грунтов. Поэтому математическое описание задач влагопереноса из одной зоны плотины в другую с учетом анизотропности грунтов является актуальной темой научного исследования.
Математическая задача о влагопереносе в теле плотины может быть решена как для изотропного грунта, если коэффициент анизотропии такого грунта невелик, то есть при рассмотрении таких конструкций плотины, в основании которой используются горизонтально укатанные слои, в том числе и из разнородных материалов. Для таких конструкций плотины коэффициент фильтрации грунта в горизонтальном направлении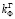 
= (2-3)
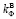(где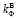 
– коэффициент фильтрации грунта в вертикальном направлении [3, с. 374–375; 5, с. 172].
Анизотропные свойства грунтов насыпных плотин необходимо тщательно изучать на основании не только геологических проб, но и математических моделей поведения грунта при влагопереносе. В модели изотропных грунтов могут при этом вноситься поправки на основании эмпирически полученных кривых депрессий, характерных именно при фильтрации влаги через анизотропные грунтовые материалы.
Цель исследования – разработка математического описания (модели) влагопереноса в насыщенной и ненасыщенной зонах насыпной плотины с учетом анизотропности грунта. При этом результаты математического моделирования – профили потенциалов влаги – необходимо сравнить (верифицировать) с существующими гидродинамическими сетками для плотин из изотропных и анизотропных грунтов.
Материалы и методы исследования
Различные исследования в области фильтрационных способностей грунтовых плотин [6–8] устанавливают канонический вид гидродинамических сеток для однородных плотин изотропной и анизотропной структуры (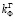
=
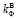). На рис. 1 представлена грунтовая плотина с плоским дренажем. На рис. 1 рассмотрены два случая: а) поведение грунта плотины при изотропной проницаемости; б) поведение грунта плотины при анизотропной проницаемости (с анизотропным дренажем) [3, с. 375].
Следует отметить, что при изотропной проницаемости плотины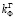 
=
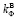, а при анизотропной проницаемости 
=
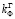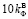[5, с. 171]. Следовательно, проницаемость грунтовых плотин в горизонтальном направлении при движении влаги по кривой депрессии от верхнего бьефа к нижнему при использовании различных анизотропных материалов может составлять на порядок больше значения 
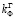. Такая ситуация фильтрации влаги через грунтовую плотину показана на рис. 1, б. Именно результаты этой гидродинамической сетки будем использовать при верификации результатов проведенного математического моделирования вопроса исследования.
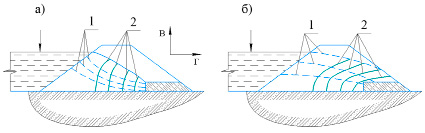
Рис. 1. Гидродинамические сетки в грунтовой плотине с плоским дренажем: а) поведение грунта плотины при изотропной проницаемости; б) поведение грунта плотины при анизотропной проницаемости; 1 – кривые депрессии; 2 – профили потенциалов влаги Источник: составлено автором по [3, с. 375]
Экспериментальные данные снижения уровня грунтовых вод в колоннах из супеси
|
Положение уровня в колонне H, м |
Изменение уровня от H1 до H2, ΔH |
Количество израсходованной воды для подъема уровня на ΔH, ΔQ |
Водоотдача δ = ΔQ / ΔHS, где S – площадь поперечного сечения колонны, м2 |
|
0,16 |
– |
– |
– |
|
0,68 |
0,52 |
0,424 |
0,036 |
|
0,84 |
0,16 |
0,496 |
0,137 |
|
0,88 |
0,04 |
0,242 |
0,268 |
|
0,91 |
0,03 |
0,192 |
0,284 |
Источник: составлено автором по [11, с. 197].
В качестве метода исследования поставленной цели выбрано математическое моделирование процесса влагопереноса в насыпной плотине с учетом анизотропности грунта и насыщенности грунта влагой. Проводятся аналитические исследования влагопереноса по сечению насыпной плотины из анизотропного грунта с учетом теоретических исследований, проведенных рядом авторов для изотропных грунтов [6–8]. Математическую задачу сформулируем следующим образом.
Габаритные размеры грунтовых насыпных плотин с последующими расчетами технических показателей и напряженно-деформированного состояния плотины являются одним из основных вопросов практики мелиоративного проектирования. В основу широко применяемой в настоящее время гидродинамической схемы расчета ГТС положено решение уравнения Буссинеска [9, с. 74]:
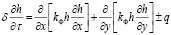, (1)
где h – расстояние от свободной поверхности грунтовых вод до водоупора, м; τ – время, сут; kФ – коэффициент фильтрации, см/сут; x, y – горизонтальные координаты, м; δ – водоотдача; q – расход грунтовых вод на испарение или интенсивность инфильтрационного питания, кг/м2·сут.
Решая задачу почвенного влагопереноса, коэффициенты kФ и δ в уравнении (1), как правило, принимают постоянными, лишь в отдельных случаях учитывается зависимость коэффициента фильтрации kФ от градиента напора, а коэффициента водоотдачи δ – от положения уровня воды в водохранилище [10, с. 771]. Однако основные параметры, входящие в уравнение (1), являются переменными величинами, а именно: водоотдача δ зависит не только от положения уровня воды относительно поверхности, но и от скорости его изменения, а также влагопроводности зоны аэрации грунтовой плотины.
В таблице приводим опытные данные водоотдачи, полученные в лабораторных условиях при медленном режиме снижения уровня грунтовых вод в колоннах из супеси [11, с. 197].
Анализируя данные таблицы, видим, что с увеличением зоны аэрации грунтовой плотины (неполного насыщения грунта плотины водой) водоотдача δ монотонно возрастает (в 8 раз, хотя среднее значение δ составляет 0,18). В принципе, передвижение влаги в насыщенной и ненасыщенной зонах плотины можно описать следующей системой дифференциальных уравнений, которая будет основана на физическом смысле уравнения (1):
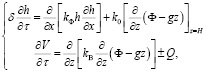(2)
где k0 – коэффициент влагопроводности уровня грунтовых вод; Ф – капиллярный потенциал влаги, Дж/кг; g – ускорение силы тяжести, м/с2; kB – коэффициент влагопроводности, кг2/Дж·cут·м; V – содержание воды в единице объема кг/м3; Q – сток или источник влаги в ненасыщенной зоне, кг/м3·сут; z – вертикальная координата, м.
Получить точное математическое решение системы дифференциальных уравнений (2) невозможно, а использование численных методов помогает получить данные, которые могут быть верифицированы и приняты во внимание.
Для упрощения поставленной задачи авторы разработали методику расчета движения влаги в насыщенной и ненасыщенной зонах грунтовой плотины (контактирующей с водой в верхнем бьефе и польдерной части плотины), учитывающая изменение профиля влажности в зоне аэрации. При отсутствии осадков, стоков (источников) предлагаем перенос влаги в насыщенной и ненасыщенной зонах описывать следующей системой дифференциальных уравнений:
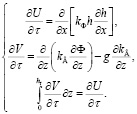(3)
здесь hn – расстояние от поверхности почвы до водоупора, м; U – содержание воды в слое hn, кг/м3.
Результаты исследования и их обсуждение
Систему дифференциальных уравнений (3) решали методом усреднения. Вначале, учитывая граничные условия, решали первое уравнение системы (3) [12], которое принимает вид
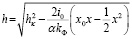, (4)
где hκ – расстояние от водоупора до уровня воды в канале, м; α – коэффициент висячести; i0 – поток на уровне грунтовых вод, кг/м2·сут; x – переменная во времени длина возмущения уровня грунтовых вод, м; x0 – координата, в которой h = h0.
Подставляя во второе выражение системы дифференциальных уравнений (3) зависимость, описывающую изменение проводимости грунта от потенциала почвенной влаги, получаем
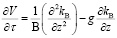, (5)
здесь kB = k0 exp (BФ) – где В – постоянная (для определения типа грунта), характеризующая степень изменение V в связи с изменением Ф.
Используя выражение (5), можно построить ряд кривых депрессий, а затем на основании полученных кривых можно построить потенциалы влаги (рис. 2), которые являются частью гидродинамической сетки, как показано на рис. 1.
На рис. 2 представлены профили (усредненные кривые) распределения капиллярных потенциалов и время их наступления, полученные в процессе опускания уровня грунтовых вод в колонне (супеси) и рассчитанные численными методами.
Решая уравнение (5) для процесса влагопереноса при соответствующих краевых условиях, получаем зависимость
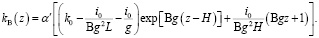(6)
Здесь α′ – поправочный коэффициент, учитывающий анизотропию грунта при деформации [13, с. 111].
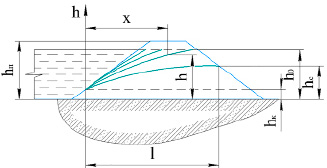
Рис. 2. Распределение расчетных и экспериментальных профилей потенциалов влаги, определенных численными методами решения уравнения (5) Источник: составлено автором
Зная распределение капиллярного потенциала влаги по глубине почвы и используя зависимость kB = f (Ф, V), строим профили распределения влажности. Время наступления соответствующих кривых депрессий при этом можно определить из эмпирического выражения
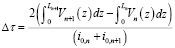. (7)
Здесь Ln – зона возмущения уровня грунтовых вод, м; Vn(z) – профиль влажности. соответствующий уровню воды по длине возмущения Ln.
В случае анизотропности профиля или слабовыраженного влагопереноса грунта зависимость kB = f (Ф) нельзя описать одной функцией kB = k0 exp (BФ). Тогда ее изменение описывается на нескольких участках, что значительно усложняет решение второго выражения, входящего в систему дифференциальных уравнений (3). В общем решение остается подобным изложенному выше.
Полученная методика в результате математического моделирования связана с аналитическими и численными методами решения краевых задач влагопереноса в дифференциальной форме для случаев опускания уровня водных масс в водохранилище при фильтрационных процессах, также эта методика может быть использована при расчетах опускания грунтовых вод в колоннах и осушения грунтов.
Сравнивая полученные профили потенциалов влаги, показанные на рис. 2 с классическими гидродинамическими сетками, представленными на рис. 1, заключаем, что в ходе математического моделирования влагопереноса в насыщенной и ненасыщенной зонах насыпной плотины при анизотропной проницаемости грунта получены профили потенциалов влаги, эквивалентные результатам исследований [3, c. 375], в которых рассматривается изотропный грунт с плоским непроницаемым (анизотропным) дренажем.
Анализ профилей потенциалов влаги (рис. 2) также показывает, что результаты теоретических исследований и полученной авторами математической модели для профилей влаги (гидродинамической сетки плотины) профили распределения потенциалов практически совпадают. Незначительные расхождения возникают из-за наложения гистерезисных явлений и точности их учета. Это указывает на возможность использования вышеизложенного подхода для прогноза режима влажности грунта плотины в процессе снижения или повышения уровня воды в водохранилище.
Заключение
В данном исследовании представлена математическая модель для влагопереноса в насыщенной и ненасыщенной зонах насыпной плотины с учетом анизотропности грунта. Рассмотрена конструкция насыпной плотины из анизотропного грунта, через которую математически смоделирован влагоперенос из насыщенной зоны (откоса плотины, контактируемый с водой) в ненасыщенную (откос плотины польдерной части). Получены профили потенциалов влаги, которые возникают в теле плотины при влагопереносе через анизотропный грунт. В математической модели впервые использован поправочный коэффициент, учитывающий анизотропию грунта при деформации во влажном состоянии. Установленные в результате математического моделирования профили потенциалов влаги для анизотропных грунтов насыпных плотин совпадают по характеру с результатами исследований, выполненных ранее (используемых в исследовании для верификации). Однако следует отметить, что могут возникать некоторые отличия из-за сложности и нестационарности процесса фильтрации – гистерезиса фильтрации и подхода его учета в модели. Установлена эмпирическая зависимость времени наступления соответствующих кривых депрессий от профилей потенциалов влаги в грунте плотины. Полученные результаты исследования могут быть использованы при проектировании плотин из анизотропных грунтов с учетом предложенной модели влагопереноса из насыщенной в ненасыщенную зону гидротехнического сооружения.
Библиографическая ссылка
Качаев А.Е., Брыль С.В. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ВЛАГОПЕРЕНОСА В НАСЫЩЕННОЙ И НЕНАСЫЩЕННОЙ ЗОНАХ НАСЫПНОЙ ПЛОТИНЫ ПРИ АНИЗОТРОПНОЙ ПРОНИЦАЕМОСТИ ГРУНТА // Научное обозрение. Технические науки. 2025. № 3. С. 5-10;URL: https://science-engineering.ru/ru/article/view?id=1507 (дата обращения: 08.06.2025).