Введение
В данной статье автор описывает методику применения псевдопараллельных вычислительных алгоритмов, позволяющую решать задачи, требующие обработки информации/вычислений/получения сигналов/изменения состояний в режиме реального времени параллельно друг с другом, но с применением электронной вычислительной машины, архитектура которой подразумевает работу в однопоточном/однопроцессорном режиме.
Автором были изучены и проанализированы существующие публикации по тематике «Параллельные вычисления» [1–3]. Анализ показал косвенное упоминание подобия псевдопараллельных вычислений некоторыми авторами вышеуказанных статей, но подробный разбор в статьях не приводится, что подчеркивает необходимость изучения и описания научным языком данной тематики для дальнейшего ее применения в промышленных средах.
Данная методика основывается на построении работы программы таким образом, при котором основной алгоритм – повторяющийся цикл с жестко заданным временем выполнения и набором счетчиков, количество которых равно количеству выполняемых задач.
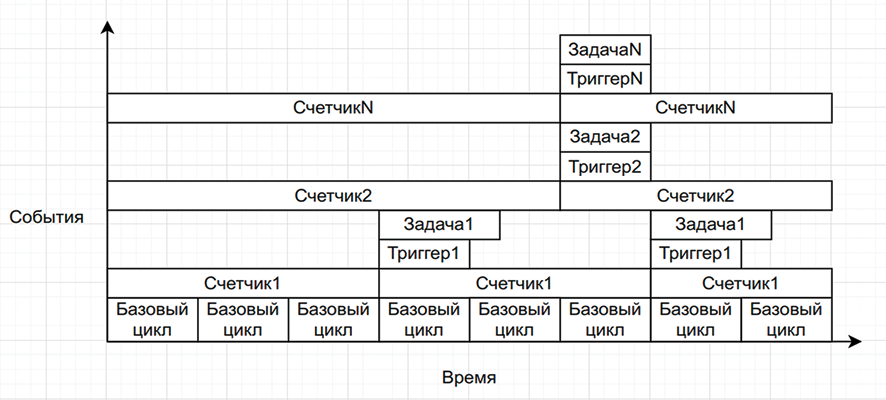
Рис. 1. Диаграмма Ганта, отражающая принцип работы псевдопараллельного алгоритма Горизонтальная плоскость является временной шкалой, вертикальная – отражает слои происходящих в тот или иной отрезок времени событий. Нижний слой содержит блоки повторения базового цикла, над ними расположены слои счетчиков, связанных с ними триггеров и выполняемых задач Источник: составлено автором на основе анализа задачи и последующего синтеза структуры целевого алгоритма
Внутри цикла реализованы проверки, базирующиеся на состоянии счетчиков и, при достижении ими определенных значений, вызывающие необходимые функции. Счетчики инкрементируются при каждом проходе цикла. Так же алгоритм поддерживает коррекцию в зависимости от затраченного на выполнение задач времени. Диаграмма работы алгоритма отражена на рис. 1.
Цель исследования – освоить и описать научным языком методику применения псевдопараллельных алгоритмов для последующего внедрения в промышленные контуры.
Материалы и методы исследования
Изначально исследования проводились автором на базе процесса разработки системы термоконтроля серверных комнат методом анализа, синтеза и моделирования, но довольно быстро были масштабированы и на другие случаи решения задач, связанных с автоматизацией различных процессов (внутренняя автоматизация организации).
В результате исследования было выявлено, что данный алгоритм имеет практическую ценность при построении автоматизированных вычислительных систем реального времени, требующих от вычислительных мощностей параллельного решения различного рода задач, легко применим и повторяем.
Для исследования автором применялись следующие технологии: микроконтроллерная платформа NodeMCU [4], DHT11, скриптовый язык программирования lua [5].
Для удобочитаемости, универсальности и простоты освоения в данной статье будут использованы примеры, реализованные на языке программирования Python [6] в силу его распространенности и легкости восприятия исходного кода.
Результаты исследования и их обсуждение
Результатом исследования является алгоритм, позволяющий реализовать параллельные вычисления на платформах, архитектурно не поддерживающих параллельный запуск нескольких процессорных команд (последовательная платформа).
Итак, непосредственно алгоритм:
1. Базовый цикл. Алгоритм строится вокруг основного цикла, выполняющегося бесконечно. Цикл имеет жестко заданный период выполнения. Внутри цикла находятся счетчики и логика их инкрементирования. Такой цикл в статье будет называться базовым циклом.
В интерпретации языка программирования Python [6] аналогом является следующий код:
import time
cyclePeriod = 0.001
counter1 = 0
counter2 = 0
counter... = 0
while(True):
counter1 += 1
counter2 += 1
counter... += 1
… код с функциональной логикой ...
time.sleep(cyclePeriod)
В приведенном примере период равен одной миллисекунде. Счетчики через 1 с примут значение 1000, через 2 с – 2000 и т.д.
2. Задачи. Условия вызова задач определяются внутри тела базового цикла. Каждая задача – функция, на выполнение которой уходит определенное количество времени и которая занимает определенное количество процессорных тактов [7]. Вызов осуществляется при достижении счетчиком функции определенного значения (срабатывает триггер). После выполнения функции счетчик сбрасывается в значение 0.
Расчет триггера выполняется следующим способом:
nтриггер = Тфункции / Тбазовогоцикла ,
где nтриггер – результирующее значение триггера, Тфункции – желаемый период запуска функции, Тбазовогоцикла – период выполнения базового цикла.
Пример, реализованный на языке программирования Python [6] в контексте кода приведенного в 1 разделе:
... тело цикла
# Задача 1 (1 раз в секунду)
if counter1 >= 1000:
print(‘1 раз в секунду’)
counter1 = 0
# Задача 2 (2 раза в секунду)
if counter2 >= 500:
print(‘2 раза в секунду’)
counter2 = 0
… тело цикла
При достижении первым счетчиком значения больше или равно 1000 будет выполнена первая задача, счетчик будет возвращен в значение 0. Аналогично отработает вторая задача при достижении вторым счетчиком значения 500 или больше.
3. Компенсация задержек. Глобальная корректировка счетчиков в результате возникновения задержек при выполнении задач является необходимостью в случае, когда программа должна выполнять задачи с соблюдением временных периодов. Например, первая задача – строго каждые 500 мс, вторая задача – строго каждые 1000 мс и т.д. [8]
За счет сокращения времени цикла достигается отсутствие сдвига из-за затрачиваемого на выполнение задач времени. Если необходимости в соблюдении жестких временных рамок при запуске задач нет, реализация данной функциональности необязательна, в таком случае периоды между запусками задач будут отличаться в зависимости от количества их вызовов и времени обработки, проще говоря время старта каждой задачи будет «плавать» в зависимости от времени, затраченного на выполнение остальных задач.
Первый этап: необходимо определить время, затраченное на выполнение полезной нагрузки задачи и зафиксировать его. Надежным и автоматическим способом является снятие временной метки непосредственно перед запуском задачи и сразу после ее выполнения. Разница временных меток позволит получит время выполнения задачи:
Тзадачи = Твыполнение – Тзапуск,
Второй этап: при срабатывании триггера и выполнении вышеуказанной задачи добавить ко всем счетчикам компенсационное значение, равное отношению Тзадачи к Тбазовогоцикла
nкомпенс = Тзадачи / Тбазовогоцикла ,
Простыми словами, время до срабатывания всех триггеров сократится на количество тактов, соответствующее времени, которое выполнялась запущенная задача. Таким образом, произойдет компенсация времени выполнения задачи за счет сокращения тактов до запуска триггеров всех задач.
На языке программирования Python [6] описанный выше алгоритм реализуется следующим образом:
...
cyclePeriod = 0.001
counter = [0, 0, 0]
# Получение времени в миллисекундах
def current_milli_time():
return round(time.time() * 1000)
# Корректировка счетчиков
def counterAdjustment(correction, counter):
counter = [x + correction for x in counter]
print(f'Корректировка: {correction}')
return counter
… внутри цикла:
# Задача 1 (1 раз в секунду)
if counter[0] >= 1000:
preMillis = current_milli_time()
print('1 раз в секунду')
… полезная нагрузка ...
counter = counterAdjustment(current_milli_time() – preMillis, counter)
counter[0] = 0
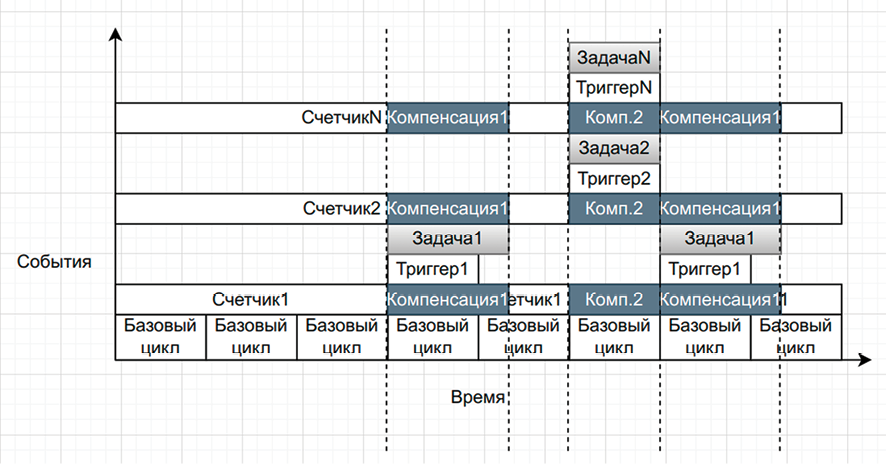
Рис. 2. Диаграмма Ганта, отражающая суть компенсации значения счетчиков при возникновении задержек во время выполнения задач. От блоков задач проведены вертикальные прерывистые линии, иллюстрирующие проекцию времени выполнения задач на счетчики Источник: составлено автором на основе реализованного алгоритма с интегрированной компенсацией времени выполнения задач
В приведенном примере Тбазовогоцикла равен 1 мс, соответственно, расчет nкомпенс достаточно прост: количество тактов на сокращение равно количеству мс, затраченному на выполнение задачи.
Принцип работы компенсационного алгоритма проиллюстрирован на рис. 2.
4. Выполнение задач в фоновом режиме или с отложенными эффектами. При выполнении кода в теле задачи нельзя использовать функции задержки (в случае Python [6] – time.sleep()), так как вызов такой функции полностью прервет выполнение программы на заданный в параметрах период, что остановит базовый цикл и нарушит принцип работы алгоритма.
При необходимости ожидания какого-либо условия или отсчета заданного периода времени внутри задачи, используется подход с флагом запуска ожидания и связкой триггер-счетчик, работающих параллельно с другими задачами и срабатывающих при выполнении заданных условий.
Пример вышеописанного алгоритма, реализованный на языке программирования Python [6]:
… Тело цикла
# Задача 3 (запускается каждые 3 секунды, ждет 10 секунд, выполняется)
if waitTaskFlag == False and counter[2] >= 3000: # Запуск ожидания
print(‘Ожидающая задача запущена’)
waitTaskFlag = True
if waitTaskFlag == True and waitCounter < 10000: # Ожидание, пока счетчик меньше 10000
waitCounter += 1
if waitTaskFlag == True and waitCounter >= 10000: # Запуск задачи по истечении 10 секунд после запуска
print(‘Ожидающая задача выполнена спустя 10 секунд после запуска’)
waitTaskFlag = False
waitCounter = 0
counter[2] = 0
… Тело цикла
Этапы алгоритма реализации задержки при необходимости ее выполнения внутри задачи
|
Шаг |
Описание |
Условия выполнения |
|
1 |
Запуск ожидания Поднимает флаг ожидания |
Если флаг ожидания опущен и триггер базового счетчика сработал (при необходимости) |
|
2 |
Ожидание Инкрементирует счетчик ожидания |
Если флаг ожидания поднят и триггер счетчика ожидания не сработал |
|
3 |
Запуск задачи Сброс флага, сброс базового счетчика и счетчика ожидания |
Если флаг ожидания поднят и триггер счетчика ожидания сработал |
Источник: составлено автором на основе подхода собственной разработки, функционирующего за счет системы, состоящей из флага запуска ожидания и связки триггер – счетчик, работающих параллельно с другими задачами и срабатывающих при выполнении заданных условий. Назначение: более структурированно представить алгоритм, описанный выше.
Алгоритм, лежащий в основе данного кода, описан более подробно в таблице.
5. Пример кода. Ниже приведен полный листинг кода программы, основанной на использовании псевдопараллельного вычислительного алгоритма.
import time
import math
cyclePeriod = 0.001
counter = [0, 0, 0]
waitTaskFlag = False
waitCounter = 0
# Получение времени в миллисекундах
def current_milli_time():
return round(time.time() * 1000)
# Корректировка счетчиков
def counterAdjustment(correction, counter):
counter = [x + correction for x in counter]
print(f’Корректировка: {correction}’)
return counter
# Основной цикл
while(True):
# Инкремент счетчика
counter = [x + 1 for x in counter]
# Задача 1 (1 раз в секунду)
if counter[0] >= 1000:
preMillis = current_milli_time()
print(‘1 раз в секунду’)
for x in range(100000):
temp = math.cos(999999)
counter = counterAdjustment(current_milli_time() – preMillis, counter)
counter[0] = 0
# Задача 2 (2 раза в секунду)
if counter[1] >= 500:
preMillis = current_milli_time()
print(‘2 раза в секунду’)
counter = counterAdjustment(current_milli_time() – preMillis, counter)
counter[1] = 0
# Задача 3 (запускается каждые 3 секунды, ждет 10 секунд, выполняется)
if waitTaskFlag == False and counter[2] >= 3000: # Запуск ожидания
print(‘Ожидающая задача запущена’)
waitTaskFlag = True
if waitTaskFlag == True and waitCounter < 10000: # Ожидание, пока счетчик меньше 10000
waitCounter += 1
if waitTaskFlag == True and waitCounter >= 10000: # Запуск задачи по истечении 10 секунд после запуска
print(‘Ожидающая задача выполнена спустя 10 секунд после запуска’)
waitTaskFlag = False
waitCounter = 0
counter[2] = 0
time.sleep(cyclePeriod)
В коде приведенной программы импортированы две библиотеки: time и math. Обе библиотеки входят в базовую поставку дистрибутива Python, применяются для работы со временем (time) и выполнения математических операций (math). Библиотеки, предназначенные для многопоточных и многоядерных вычислений [9] (например, популярные библиотеки threads и multiprocessing), в программе не использованы.
Заключение
Разработанная и описанная автором статьи методика, построенная на псевдопараллельном подходе к разработке программного обеспечения, включающая такие понятия, как базовый цикл, счетчики, триггеры, корректировка и задачи, успешно зарекомендовала себя при практическом использовании в промышленной среде и рекомендуется автором к освоению и повторению.
Новизна результатов исследования подтверждается отсутствием ранее опубликованных минимально схожих материалов, столь подробно описывающих применение подобных алгоритмов в промышленной эксплуатации.
Представленный псевдопараллельный алгоритм применим в различных встраиваемых системах, требующих использования микроконтроллерных вычислительных платформ, но также может быть применен и при разработке программного обеспечения для других видов ЭВМ, например, при невозможности использования по ряду причин библиотек, реализующих многопоточные или многоядерные вычисления.
Библиографическая ссылка
Лелейкин С.С. МЕТОДИКА ПРИМЕНЕНИЯ ПСЕВДОПАРАЛЛЕЛЬНЫХ АЛГОРИТМОВ // Научное обозрение. Технические науки. 2025. № 4. С. 11-16;URL: https://science-engineering.ru/ru/article/view?id=1516 (дата обращения: 07.02.2026).
DOI: https://doi.org/10.17513/srts.1516


 science-review.ru
science-review.ru