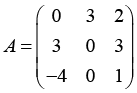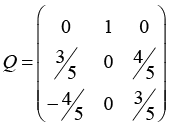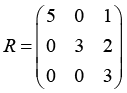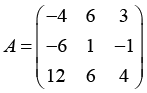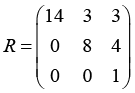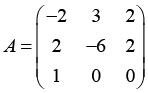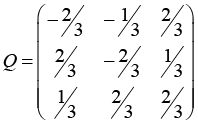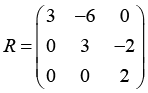science-review.ru
Введение
QR-разложение матриц является одним из фундаментальных инструментов линейной алгебры и вычислительной математики. Оно находит широкое применение в решении переопределенных систем линейных уравнений, вычислении собственных значений и многих других задачах [1; 2]. Понимание алгоритмов построения QR-разложения, таких как метод отражений и метод вращений, а также их геометрической интерпретации является важной составляющей математической подготовки студентов технических специальностей [3].
Однако процесс изучения и преподавания этой темы сопряжен с определенными трудностями. Сложность вычислительных процедур, необходимость визуализации геометрических преобразований и обеспечение эффективной практической отработки навыков студентами требуют специальных подходов. Традиционные методы обучения, основанные на ручных вычислениях, часто не позволяют в полной мере продемонстрировать эффективность и суть алгоритмов, кроме того, проверка результатов выполнения заданий по QR-разложению вручную является трудоемкой задачей для преподавателя, особенно при большом потоке студентов.
В статье рассматривается инструментарий для интерактивного представления QR-разложения на платформе ИОС Nomotex [4; 5]. Как было отмечено в работе [6], внедрение специализированных компьютерных средств визуализации позволяет сделать абстрактные алгебраические преобразования наглядными и интерактивными. Автоматизация процессов генерации вариативных индивидуальных заданий и проверки ответов студентов способна кардинально повысить эффективность обучения и снизить нагрузку на преподавателя [7-9].
Цель исследования – разработать программный комплекс интерактивной визуализации различных методов нахождения QR-разложения матрицы и реализовать алгоритм автоматизации контроля знаний по теме «QR-разложение».
Материалы и методы исследования
QR-разложение матрицы – это метод линейной алгебры, позволяющий представить матрицу A в виде произведения двух матриц: Q и R, где Q – ортогональная (или унитарная в случае комплексных чисел) матрица, состоящая из столбцов, которые являются ортонормированными векторами, а R – верхняя треугольная матрица. Для матрицы A размера m×n (где m ≥ n) разложение выглядит так:
A = QR.
При нахождении QR-разложения для матриц маленького размера удобно использовать ортогонализацию Грама – Шмидта: столбцы матрицы A интерпретируются как векторы ai, далее на основе этой системы векторов находится ортонормированная система векторов qi, которые являются столбцами матрицы Q, а матрица R состоит из коэффициентов разложения векторов qi по векторам ai. При решении задач без использования ЭВМ этот метод является предпочтительным.
В программной реализации чаще всего используются два метода: вращений и отражений. Ключевое преимущество обоих методов заключается в их численной устойчивости. Поскольку преобразования Гивенса и Хаусхолдера являются ортогональными, они не усиливают вычислительную погрешность. Классический и модифицированный методы Грама – Шмидта существенно проигрывают в устойчивости. Из-за ошибок округления вычисляемые векторы qi быстро теряют ортогональность, особенно если матрица A плохо обусловлена. Методы же вращений и отражений идеально сохраняют ортогональность в арифметике с плавающей точкой, что критически важно для итерационных алгоритмов, например QR-алгоритма для поиска собственных значений.
Результаты исследования и их обсуждение
В рамках данного исследования авторами были разработаны специализированные интерактивные программные модули, реализованные на платформе ИОС Nomotex, обеспечивающие геометрическую интерпретацию двух ключевых методов QR-разложения: вращений Гивенса и отражений Хаусхолдера.
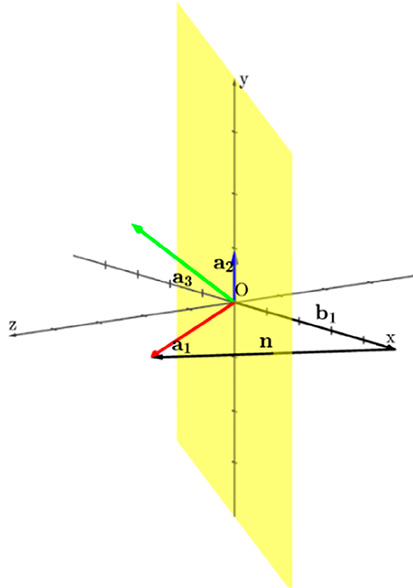
Для метода вращений был разработан интерактивный пример, позволяющий наблюдать, как последовательность элементарных вращений в координатных плоскостях постепенно преобразует исходную матрицу к верхнетреугольному виду. Особое внимание уделяется визуализации преобразования столбцов матрицы: каждый столбец трактуется как вектор в многомерном пространстве, и пользователь может наблюдать, как эти векторы постепенно преобразуются в систему, которой будет соответствовать верхнетреугольная матрица. Для этого вектор a1 должен оказаться на оси Ox, вектор a2 в плоскости Oxy, а вектор a3 может быть произвольным. На рисунке 1 можно видеть исходное положение векторов, задаваемых столбцами матрицы A.
Далее в примере демонстрируется преобразование поворота, которое приводит матрицу к верхнетреугольному виду. В данном случае необходимо «обнулить» только элемент в третьей строчке и первом столбце, это можно сделать с помощью поворота относительно оси Oy.
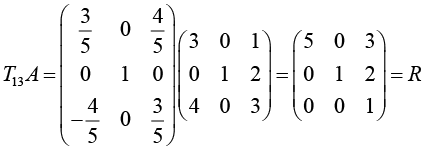
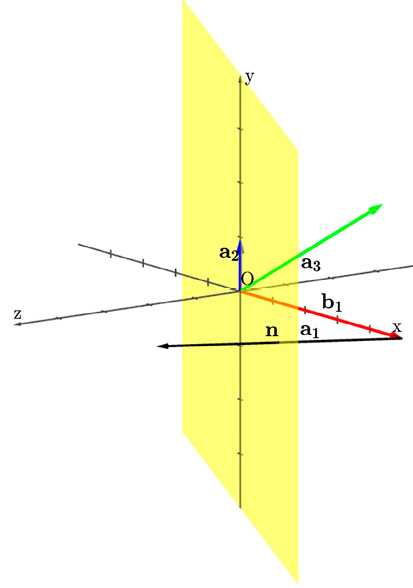
Все преобразования можно увидеть на графике в виде анимации, что наглядно демонстрирует приведение матрицы к верхнетреугольному виду. На рисунке 2 показано итоговое положение векторов.
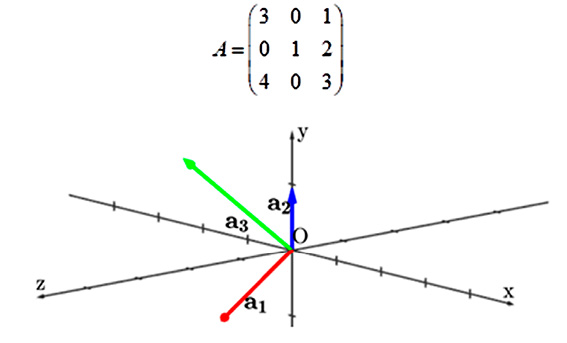
Рис. 1. Геометрическая визуализация матрицы, которую необходимо привести к верхнетреугольному виду
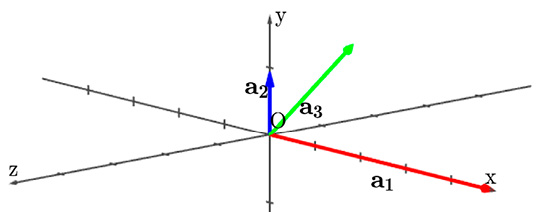
Рис. 2. Геометрическая визуализация матрицы, приведённой к верхнетреугольному виду
|
|
|
Рис. 3. Отражение векторов a1, a2, a3
Для метода отражений также была создана визуализация, которая позволяет проследить геометрический смысл преобразования, приводящего матрицу к верхнетреугольному виду. На рисунке 3 слева можно видеть исходное положение векторов, координаты которых задаются той же матрицей A, и плоскость, относительно которой нужно отразить вектор a1 = (3 0 4)T, чтобы у него обнулились все координаты, кроме первой.
Матрица такого преобразования вычисляется по формуле
,
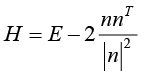где E – единичная матрица,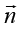 
– нормаль к плоскости, относительно которой отражаются векторы. Тогда для матрицы A такое преобразование будет описываться матрицей
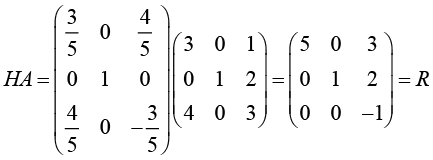
Итоговый вид QR-разложения можно найти, если умножить обе части равенства на матрицу, обратную к H, причём, так как она является ортогональной, то H–1 = HT.
В рамках разработанного учебного модуля также была реализована уникальная возможность интерактивного исследования процесса QR-разложения. Студенты получают доступ к интуитивно понятному интерфейсу, где могут ввести произвольную матрицу и наблюдать весь процесс её преобразования в режиме реального времени. Данный подход позволяет преодолеть традиционные трудности в понимании QR-разложения. Студенты не просто запоминают алгоритмические шаги, а формируют глубокое интуитивное понимание геометрической сути процесса [10]. Наблюдая, как произвольно заданная матрица шаг за шагом преобразуется в верхнетреугольную, учащиеся устанавливают прочную связь между алгебраическими операциями и их геометрическим смыслом.
Автоматическая генерация условий
При автоматической генерации заданий такого вида необходимо в первую очередь учитывать арифметическую сложность решения и постараться минимизировать вероятность арифметической ошибки [11; 12]. Этого можно добиться, если сформулировать условия таким образом, чтобы в ходе решения не появлялись сложные, несократимые дроби, а также выражения с корнем. Для задачи нахождения QR-разложения исходную матрицу A можно сгенерировать, если подобрать произвольную ортогональную матрицу Q и верхнетреугольную матрицу R и перемножить их. Но элементы ортогональной матрицы чаще всего бывают корнями, и, как следствие, процесс нахождения такой матрицы будет подвержен большому количеству ошибок.
Авторами был предложен и реализован следующий алгоритм, который позволяет генерировать ортогональные матрицы с «удобными» коэффициентами для нахождения QR-разложения с помощью ортогонализации Грама – Шмидта.
1. Подбираются такие целые значения m и n, которые образуют пифагорову тройку, то есть сумма квадратов этих чисел равняется квадрату третьего целого числа. Это поможет избежать корней при нормировке векторов.
2. Тогда ортогональную матрицу Q можно в общем виде записать таким образом:
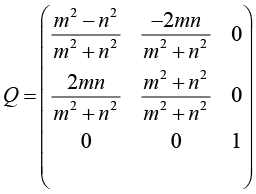
3. Далее для разнообразия матриц Q можно переставить столбцы или строки матрицы местами, транспонировать матрицу и умножить на исходную. По свойствам также будет получаться ортогональная матрица.
4. Матрица R подбирается как матрица со всеми диагональными элементами, равными 1 и со случайными значениями a, b, c, таким образом, чтобы значения матрицы A были целыми числами.
.
Ниже приведены результаты работы алгоритма.
Результаты работа алгоритма по генерации условий
|
Условие задачи. Матрица A |
Ответ. Матрица Q |
Ответ. Матрица R |
|
|
|
|
|
|
|
|
|
|
|
|
Разработанный алгоритм позволяет автоматически генерировать различные условия, и при этом решение задачи не сопровождается сложными арифметическими вычислениями, что позволяет студентам сосредоточиться на ходе решения задачи.
Автоматическая проверка
Одним из ключевых преимуществ современных образовательных платформ является мгновенная обратная связь [13; 14]. За этим стоит система автоматической проверки ответов, которая сравнивает решение пользователя с эталонным [15]. Подавляющее большинство автоматических проверок построено по принципу «всё или ничего». Это означает, что ответ учащегося признается либо абсолютно верным, либо полностью неверным [13; 14]. Система ищет точное совпадение с заранее заложенным правильным ответом. При таком подходе невозможно оценить частично правильное решение. Например, если студент правильно выстроил логику и совершил вычислительную ошибку в последнем действии, система не засчитает ему правильные этапы рассуждения – она увидит лишь неверный итоговый ответ и поставит «0» [14; 15].
Для решения этой проблемы при проверке задачи на нахождение QR-разложения был разработан алгоритм на базе информационно-образовательной среды Nomotex, который позволяет проверять не только итоговый ответ, но и ход решения, и оценивать задачу поэтапно. В рамках проверки знаний по данной теме студентам предлагается найти QR-разложение с помощью ортогонализации Грама – Шмидта, и в качестве ответа указать матрицы Q и R. Введённый студентом ответ проверяется по следующему алгоритму.
1. Каждый столбец матрицы Q проверяется отдельно, так как является результатом последовательной ортогонализации Грама – Шмидта. Баллы начисляются за каждый верно найденный вектор.
2. Матрица R проверяется проверкой по формуле A = QR, где A – это матрица, заданная в условии, а Q – матрица, введённая студентом.
Таким образом, баллы начисляются за каждый верно найденный столбец матрицы Q и за правильно посчитанную матрицу R, что позволяет начислять баллы за частично верный ответ, а также указать студенту на шаг решения, в котором, вероятно, была допущена арифметическая ошибка.
Заключение
В процессе работы была достигнута поставленная цель: разработан комплекс инструментов, позволяющий наглядно продемонстрировать геометрическую сущность методов Гивенса и Хаусхолдера для нахождения QR-разложения матриц. Это позволяет студентам не только следовать алгоритму вычислений, но и интуитивно понимать, как последовательные вращения или отражения приводят матрицу к верхнетреугольному виду. Также был реализован алгоритм автоматической генерации индивидуальных заданий по QR-разложению, успешно формирующий матрицы, решение которых не перегружено вычислительными трудностями. Студенты могут отрабатывать навыки на множестве разнообразных примеров, при этом внимание сосредоточено на сути метода, а не на ручном упрощении дробей. Была реализована система автоматизированной пошаговой проверки решений: она предоставляет мгновенную обратную связь и частично оценивает правильность каждого этапа разложения. Этот подход к контролю знаний более гибкий и справедливый по сравнению с принципом «всё или ничего», так как поощряет верные действия даже при наличии отдельных ошибок.
Внедрение разработанных средств в учебный процесс показало, что они повышают наглядность и интерактивность изучения линейной алгебры. Преподаватели отмечают сокращение временных затрат на проверку типовых задач благодаря автоматической оценке, а у студентов наблюдается рост интереса к теме за счёт игровой формы представления алгоритмов. Подход, описанный в статье, может быть распространён и на другие разделы высшей математики. В дальнейшем планируется накопление статистики об успеваемости студентов и сравнительный анализ с традиционными методами обучения, что позволит количественно оценить достигнутый эффект. Авторы полагают, что сочетание интерактивной визуализации и автоматизации оценки является перспективным направлением развития электронных курсов по математике.
Конфликт интересов
Библиографическая ссылка
Зубарев К.М., Киреева Е.А., Дерябина Г.С., Милехина Е.Н., Волков В.Ю. ОСОБЕННОСТИ ИЗУЧЕНИЯ QR-РАЗЛОЖЕНИЯ В ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ NOMOTEX // Научное обозрение. Технические науки. 2025. № 5. С. 19-24;URL: https://science-engineering.ru/ru/article/view?id=1522 (дата обращения: 02.02.2026).
DOI: https://doi.org/10.17513/srts.1522