Научный журнал

Научное обозрение. Технические науки

ISSN 2500-0799

ПИ №ФС77-57440

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ибраев И.К. 1 Ибраева О.Т. 1

---

1 РГП «Карагандинский государственный индустриальный университет» Министерства образования

Приведена математическая модель, описывающая изменение температуры металла в процессе наполнении изложницы, которая позволяет рассчитать предельно-допустимый перегрев и температуру металла в ковше перед разливкой, с учетом планируемой скорости разливки. Предложенная математическая модель достаточно хорошо описывает изменение температуры металла в процессе наполнения изложницы. Промышленные исследования с использованием математической модели позволили выявить влияние на температуру металла при наполнении изложницы таких факторов, как линейной скорости наполнения изложницы, массы слитка, выраженной через отношения периметра к площади боковой поверхности изложницы, продолжительности наполнения изложницы до заданного уровня налива, а также исходного перегрева металла в ковше перед разливкой.

Статья в формате PDF

0 KB

дефект слитка и поверхности проката

перегрев

температура разливки

запороченность поверхности

вторичное окисление

температура ликвидус

1. Грузин В.Г. Температурный режим литья стали. – М.: Государственное Научно-техническое издательство по черной и цветной металлургии. – 1962. – С. 155–160.

2. Кочо В.С., Коробко И.М. и др. Непрерывный контроль температуры при разливке стали // Труды I конференции по стальному слитку: Разливка стали и формирование слитка. М.: Металлургия, 1966. – С. 260–268.

3. Микульчик А.В. Непрерывный замер температуры жидкой стали в промежуточных ковшах при разливке стали в вакууме // Труды III конференции по слитку: Проблемы стального слитка. – М.: Металлургия, 1969. – С. 316–317.

4. Козлов Ф.В. Изменение температуры металла при разливке стали // Труды НТО ЧМ. М.: Металлургиздат, 1955. – т. 5.

5. Смирнов А.Н., Неделькович Л. И др. Расчет температуры ликвидус // Сталь. – 1996. – № 3 – С. 15–19.

Около 80 % дефектов поверхности листового проката приходятся на дефекты сталеплавильного производства, а точнее на дефекты, возникающие при разливке и кристаллизации низкоуглеродистой стали в изложнице. Технологический режим разливки стали должен обеспечивать получение слитков стабильного высокого качества – с достаточной толщиной и плотной наружной беспузыристой коркой, хорошим качеством наружной поверхностью слитка, небольшой рослостью, низким содержанием и равномерным распределением неметаллических включений, оптимальной формой и плотной головной поверхности и малой степенью ликвации примесей. Для обеспечения условий получения слитков требуемого качества необходимо исследовать и описать физико-химические процессы возникновения причин и условий, вызывающих образование как внутренних, так и поверхностных дефектов формирующегося слитка и предложить новые технические решения по устранению запороченности слитков низкоуглеродистой стали.

Температура разливки является одной из наиболее важных параметров, влияющих на качество слитков: развитие усадочных пустот и пористости в слитке, развитие процессов кристаллизации и сегрегации, толщину и плотность корочки слитка низкоуглеродистой кипящей стали и запороченности поверхностными и внутренними дефектами.

Целью работы – определить предельно-допустимый уровень температур металла в изложницах, обеспечивающих минимальную запороченность проката поверхностными дефектами и установить оптимальные температурно-временные параметры выпуска, доводки и разливки стали на основе данных о температуре металла в изложнице.

Экспериментальная часть (теоретическая часть)

На процесс образования корочки окисной плены при заполнении изложницы металлом помимо физико-химических процессов (вторичное окисление) большое влияние оказывают теплофизические процессы [1–5]. Образование пленки окислов на поверхности жидкого металла, находящегося в контакте с атмосферой, происходят постоянно, однако образование дефектов происходит в том случае, когда пленка (корка) находится в твердом состоянии. При анализе механизма образования поверхностных дефектов следует исходить из условия одновременного протекания двух следующих процессов: окисления и охлаждения жидкого металла. Большую роль в формировании поверхности слитка играют процессы, протекающие на границе раздела жидкая сталь – атмосфера – изложница, и главным образом условия существования мениска.

Разливка стали сопровождается развитием больших, открытых для взаимодействия с атмосферой, поверхностей металла, что неизбежно приводит к вторичному окислению и охлаждению металла. Изучение гидродинамических характеристик разливки стали и проведенные на их основании расчеты [2, 4] показали, что наиболее благоприятные условия для вторичного окисления и охлаждения металла создаются в процессе подъеме металла в изложнице. Несмотря на то, что общая поверхность контакта металла в изложнице меньше поверхности струи почти в 2 раза, продолжительность контакта металла с атмосферой почти в 40 раз больше.

Одновременно с процессами окисления поверхности металла при подъеме его в изложнице с образованием окислов железа, марганца, кремния и алюминия отмечается прогрессивное снижение температуры поверхностных объемов металла. Потери тепла происходят как в результате теплоотдачи к стенкам изложницы, так и в результате и вследствие излучения с поверхности металла в окружающее пространство. На отвод тепла от поверхностных объемов металла влияют множество факторов, основные из которых – площадь поперечного сечения слитка, периметр охлаждаемой поверхности, масса и размеры слитка, скорость и температура разливки стали и коэффициент теплопередачи к стенкам изложницы.

Для устранения образования дефектов на поверхности формирующегося слитка, режим разливки должен быть подобран таким образом, чтобы тепло перегрева стали сохранялось до момента подхода металла до заданного уровня наполнения изложницы.

Как показали результаты исследований, тепло перегрева расходуется на прогрев стенок изложницы и на излучение с открытой поверхности металла по мере подъема его в изложнице. Если тепло перегрева из верхних слоев поднимающегося металла расходуется раньше окончания наполнения изложницы, то на открытой поверхности образуется корка, а на слитке возникают завороты и плены.

Отвод тепла перегрева зависит от многих факторов, основные из них: площадь поперечного сечения изложницы, периметр охлаждающейся поверхности, масса и геометрические размеры слитка, скорость и температура разливки.

Для выбора обоснованного температурно-временного режима разливки необходимо проанализировать потери тепла (перегрева) металла в процессе наполнения изложницы.

Рассмотрим тепловой баланс подвижного элемента объема жидкой стали (dh) по высоте слитка. Количество тепла dQст отдаваемого элементарным объемом жидкого металла стенкам изложницы за промежуток времени dτ, составит:

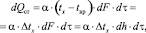(1)

где Δtх = tх – tкр – величина перегрева стали над точкой ликвидуса в рассматриваемом сечении слитка, °С; dF = Pdh – площадь боковой поверхности охлаждения выделенного элементарного объема, м2; P – периметр поперечного сечения слитка, по которому происходит теплообмен с изложницей, м

Снижение энтальпии металла за это время будет равно

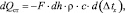(2)

где Fdh – объем элемента, м3; F – площадь сечения изложницы, м2; ρ – плотность стали, кг/м3; c – удельная теплоемкость стали, ккал/(кг•град).

Приравнивая уравнения (1) и (2), получаем дифференциальное уравнение с разделяющимися переменными.

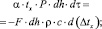(3)

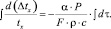(4)

Интегрируя полученное равенство и произведя небольшую подстановку имеем

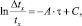(5)

где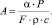

Константу интегрирования определяем из начальных условий разливки стали. В момент поступления жидкой стали в изложницу, когда τ = 0, перегрев жидкой стали равен начальному перегреву стали, т.е.

Δtx = Δtраз = tраз – tкр.

Отсюда следует

С = lntраз.

Подставляя значение константы интегрирования в уравнения (5), получаем зависимость:

(6)

Связь между величиной оставшегося перегрева в движущемся слое стали и величиной исходного перегрева стали при входе в изложницу может быть установлена путем следующего преобразования:

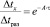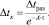или (7)

Величина Δtx в последнем уравнении характеризует тот перегрев, который остался в рассматриваемом слое стали при перемещении его, на какое то расстояние от дна изложницы. При этом температура металла в этом слое равна

Δtx = tx – tкр или 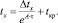(8)

Отсюда, зная остаточный перегрев металла в изложнице по наполнению заданного уровня налива в изложнице можно определить расчетную температуру металла, т.е.:

tx = tкр + Δtx.

Чтобы определить ту величину, на которую остыл подвижный элемент за время перемещения от дна изложницы до заданной высоты, необходимо от величины исходного перегрева Δtраз отнять величину оставшегося перегрева в стали Δtх, т.е.

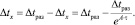(9)

Такое снижение температуры расплава наблюдалось бы в том случае, если от поступающей в изложницу стали отводилось бы тепло только на перегрев стенок изложницы. В реальных условиях разливки значительная часть тепла от жидкой стали расходуется на излучение открытой поверхностью металла в изложнице.

Эти потери тепла в окружающую среду подсчитываются:

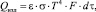(10)

где ε – коэффициент лучеиспускания открытой поверхности металла в изложнице, равной 0,53; σ – константа излучения абсолютно черного тела, равная 0,082.10–8 ккал/(м2•мин•К); F – площадь открытой поверхности металла в изложнице, м2; dτ – время перемещения (излучения) открытой поверхности металла, мин; Т – абсолютная температура поверхности металла, К.

Верхние поднимающиеся в изложнице слои стали обычно быстро теряют свое тепло. Температура открытой поверхности металла близка к температуре затвердевания стали.

Если от количества тепла, заключенного в подвижном элементе объема жидкой стали отнять тепло, теряемое на излучение, то оставшееся тепло в том же объеме жидкой стали будет определять величину перегрева, который еще остался в металле

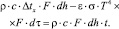(11)

Подставляя из уравнения (8) величину перегрева стали Δtx, который остался в металле после отдачи тепла стенкам изложницы, получаем:

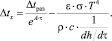
Учитывая, что dh/dΔ = w получаем

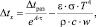(12)

где w – линейная скорость разливки, м/мин.

Тогда текущую температуру металла в конце наполнения изложницы можно определить из следующего выражения:

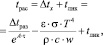(13)

где Δtраз – исходный перегрев металла в ковше перед разливкой и подсчитывается по выражению (14):

Δtраз = Tвып – Tлик – Δtковш, (14)

где Δtковш – потери температуры металла в ковше за время выпуска, обработки металла и выдержки в ковше, вычисляемая по уравнению (15)

Δtковш = Tвып – Tудм; (15)

откуда

Δtраз = Tудм – Tлик. (16)

Приведенная система уравнений (13)–(16) является математической моделью, описывающая изменение температуры металла в процессе наполнения изложницы металлом. Полученная модель позволяет выявить влияние на температуру металла при наполнении изложницы таких факторов, как линейная скорость наполнения изложницы (w), массы слитка, выраженной через отношение периметра к площади боковой поверхности изложницы (Р/S), продолжительности наполнения изложницы до заданного уровня налива (w), а также исходного перегрева металла в ковше перед разливкой (Δtраз).

Используя приведенную модель изменения температуры металла в процессе наполнения изложницы можно определить оптимальный перегрев металла над температурой ликвидус в коше перед разливкой. Если принять, что перед подходом металла к заданному уровню налива все тепло перегрева израсходовано на прогрев стенок изложницы и на излучение, т.е. когда tx = 0, то оптимальная величина перегрева стали, обеспечивающего разливку с чистым зеркалом:

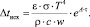(17)

В качестве абсолютной температуры металла Т принимаем температуру ликвидус для данного состава стали.

Аналогичное выражение предельно допустимого исходного перегрева металла в ковше перед разливкой получается из условия равенства текущей температуры металла в конце наполнения изложницы и температуры начала кристаллизации, т.е. tx = tлик

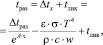
при tрас = tлик получаем

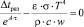
или

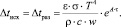
Анализ полученного выражения (17) показывает, что допустимый перегрев металла перед поступлением в изложницу определяется условиями разливки стали, т.е. линейной скоростью разливки (w), хим. составом стали (tлик) и параметрами слитка (изложницы) P/S.

Из всех параметров формул (13) и (17) неопределенным остается коэффициент теплоотдачи от металла к поверхности изложницы (α). Для определения неизвестного коэффициента, для условий разливки в крупнотоннажные листовые изложницы сверху, были проведены опытно-промышленные плавки с измерением температуры металла в конце наполнения изложницы.

Среднюю степень перегрева стали над температурой ликвидус рассчитывали по выражению (14). Измерив температуру металла в изложнице после заданного уровня налива из выражения (13) рассчитывали неизвестный коэффициент суммарной теплоотдачи от жидкого металла к стенкам изложницы и в окружающее пространство. Коэффициент α изменялся в пределах 43,0–48,3 ккал/(м2•мин•град). Для дальнейших исследований приняли суммарный коэффициент теплоотдачи α = 45 ккал/(м2•мин•град). Остаточный перегрев и расчетную температуру металла в изложнице после заполнения до заданного уровня налива рассчитывали по выражениям (13)–(16).

Результаты исследования и их обсуждение

Анализ теплотехнических условий формирования слитка, рассмотренные выше показывают, что потери тепла перегрева в процессе наполнения изложницы складываются из потерь тепла на прогрев изложницы (18) и потерь излучением зеркала металла в процессе подъема металла в изложнице (19)

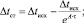(18)

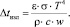(19)

Анализ потерь тепла перегрева в процессе наполнения изложницы показывает, что основная доля потерь приходится на потери тепла излучением и определяется только линейной скоростью разливки (рис. 1). Так, потери температуры (тепла перегрева) на прогрев изложницы составляют 4–5 °С при разливке через стакан 80/60 мм и 2–3 °С при разливке через стакан диаметром 90/80 мм. В то время, потери тепла перегрева излучением зеркалом металла – 20–25 °С при разливке через стакан диаметром 80/60 мм и 10–15 °С через стакан диаметром 90/80 мм. Столь существенная разница в потерях тепла перегрева при разливке через стакан 80/60 и 90/80 мм объясняются разными скоростями наполнения металлом изложниц.

Результаты опытных плавок с замерами температуры металла в изложнице в трех точках по длине состава (начальных, средних и конечных слитков) указывает на существование температурной неоднородности по длине разливочного состава, составляющее 6–12 °С (рис. 2).

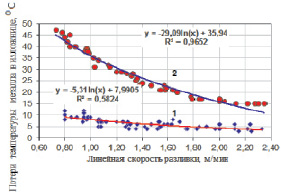
Рис. 1. Влияние скорости разливки на потери температуры металла в процессе наполнения изложницы излучением (1) и на прогрев стенок излучением (2)

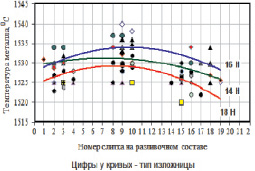
Рис. 2. Характер изменения температуры металла в изложнице в конце ее наполнения по длине разливочного состава

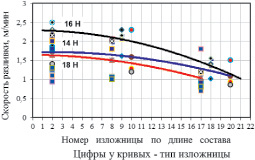
Рис. 3. Характер изменения скорости разливки по длине разливочного состава

Установленный характер снижения температуры металла в изложнице на конечных слитках состава теоретически обосновывается уменьшением линейной скорости разливки (рис. 3) и увеличением потерь тепла перегрева металла в процессе наполнения изложницы.

Существенные потери тепла перегрева при наполнении изложницы при разливке с пониженными скоростями объясняют и более низкие значения температур металла в изложнице, в особенности, конечных слитков состава, что в принципе объясняет более повышенную запороченность «пленой» конечных слитков пленой.

Сравнительный анализ расчетного перегрева по уравнению (17) с фактическим перегрев стали в ковше перед разливкой показан на рис. 4.

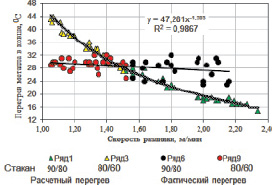
Рис. 4. Взаимосвязь перегрева металла в ковше со скоростью разливки

Из рис. 4 видно, что фактический перегрев характеризуется широким полем разброса и слабой зависимостью от линейной скорости разливки стали. Причем, при разливке стали через стакан – коллектор диаметром 80/60 мм при линейной скорости менее 1,4 м/мин, фактический перегрев находится ниже предельно-допустимого уровня, т.е. в этой области мы, как правило, имеем температуру металла в изложнице менее температуры начала кристаллизации (tлик).

Это подтверждается частотным распределением замеренных температур металла в изложнице, где доля плавок с температурой металла в изложнице менее температуры ликвидус (tизл < tлик) составляет 47 %.

Наоборот, при разливке стали через стакан диаметром 90/80 мм при линейной скорости более 1,7 м/мин, фактический перегрев превышает предельно-допустимый. Здесь, в этой области, как правило, имеем температуру металла в изложнице выше температуры ликвидус.

Это подтверждается частотными распределениями измеренных температур металла в изложнице, где доля таких плавок соответственно составляет 69,61 и 81,11 %.

Зная предельно допустимый перегрев металла в ковше перед разливкой можно установить и оптимальную температуру стали в ковше перед разливкой, с учетом планируемой линейной скорости разливки и типоразмера изложницы.

Таким образом, установлено, что на практике при выборе температуры металла в ковше не учитывается линейная скорость разливки.

Исходя из выражения Δtисх = Тковш – tлик, температура металла в ковше перед разливкой определяется по выражению (20):

Tковш = Δtисх + tлик. (20)

Выводы

Таким образом, предложенная математическая модель достаточно хорошо описывает изменение температуры металла в процессе наполнения изложницы. При использовании математической модели можно выявить влияние на температуру металла при наполнении изложницы таких факторов, как линейной скорости наполнения изложницы (w), массы слитка, выраженной через отношения периметра к площади боковой поверхности изложницы (P/S), продолжительности наполнения изложницы до заданного уровня налива (τ), а также исходного перегрева металла в ковше перед разливкой (Δtраз).

Библиографическая ссылка