На протяжении нескольких лет в учебных заведениях стремительно развиваются такие научные направления, как представление информации в виде графических данных и визуальная аналитика. Количество исследований в данных направлениях возрастает, так как расширяется спектр их применения. Представление информации в виде графических данных является одной из наиболее наукоемких областей современных информационных технологий.
К способам представления информации в виде графических данных можно отнести графики, таблицы, отчеты, схемы и так далее.
Представление информации в виде графических данных рассматривалось как вспомогательное средство при анализе экспериментальных данных в физике, хотя как теоретические, так и практические исследования позволяют говорить о ее самостоятельной роли.
В нашей работе мы применили программу 3DFieldPro (или 3DField), которая использует карты глубины, представляющие собой записанные в файл расстояния точек, расположенных на поверхности объектов до камеры, а также 3DFieldPro является программой контуров и обработки 2D/3D данных. Эта программа позволяет конвертировать данные в контурные карты, поверхности и объемные схемы.
В нашем исследовании мы использовали следующие возможности программы 3DFieldPro (или 3DField), а именно:
− интерполирование данных на сетку;
− возможность показывать месторасположение точек данных на плоскости и их значений относительно друг друга;
− графическое представление изображение в 2D/3D числовых массивов данных;
− построение карт изолиний на основе числовых данных;
− редактирование полученных изображений в соответствии c предъявляемыми к ним требованиями;
− экспорт созданных карт любого размера в документы текстового редактора;
− возможность создавать трехмерную проекцию;
− возможность создавать группу изолиний с соответствующими коэффициентами;
− возможность определять длину изолиний;
− возможность определять площадь сечения объекта, ограниченной данной изолинией;
− возможность определять объем поверхности объекта, объем объекта;
− трансформация отсканированного графика в цифровую форму;
Цель исследования: проведение компьютерной визуализации снимков Солнца, гелиограмм, взятых с соответствующих сайтов. Использование компьютерных программ позволяет получать изменения периметров объектов радиоисточников над пятнами и позволяет получать изменения площадей радиопятен [1], площадей поверхностей образований, что представляет собой интегральные потоки излучения в центральной части и всей области в целом, позволяющие получать объемы областей.
Материалы и методы исследования
Материалом исследования являются снимки поверхности Солнца с радиогелиографа Nobeyama, длина волны которых составляет 1,76 см с пространственным разрешением порядка 10″, а также снимки, полученные в солнечной обсерватории SDO. Мы рассматривали солнечные пятна, которые являются активными образованиями на фотосфере Солнца, температура которых ниже температуры фотосферы, магнитное поле достигало порядка нескольких тысяч Гаусс. Интервалы наблюдений составляли от 1 мин до 10 мин. Гелиограммы должны быть достаточно высокого качества, чтобы уровень интенсивности невозмущенной фотосферы Солнца был одинаковый. Это проверялось с помощью программы Adobe Photoshop CS5.
Результаты исследования и их обсуждение
Для примера на рис. 1 представлен снимок гелиограммы для примера, полученный 28 февраля 2017 г.
На рис. 2 представлены изменения периметра одного и того же объекта, полученного по снимкам Nobeyama и SDO. Корреляция двух кривых близка к единице, характер кривых по данным «Нобеяма» и SDO практически одинаков. Разность фаз во всех точках пространства постоянна, что говорит о когерентности волн, то есть источник колебаний один и тот же, природа колебаний одинакова.

Рис. 1. Фрагмент снимка Солнца (28.02.2017)
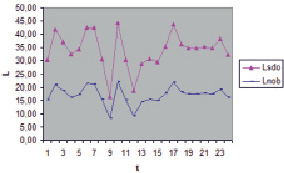
Рис. 2. Ход кривых длин изолинии солнечного пятна
В таблице впервые приведены данные для солнечного пятна, наблюдавшегося 01.02.1998 г.
Параметры тени и полутени солнечного пятна
|
Lп – длина изолинии полутени |
Lт – длина изолинии тени |
Lп/Lт |
Sп – площадь полутени |
Sт – площадь тени |
Sп/Sт |
Vп – объем полутени |
Vт – объем тени |
Vп/Vт |
|
65,3882 |
54,3502 |
1,2 |
286,746 |
197,186 |
1,45 |
67029,7 |
48206,3 |
1,39 |
|
66,6326 |
54,3502 |
1,2 |
296,262 |
197,186 |
1,5 |
68235,8 |
48206,3 |
1,41 |
|
65,3702 |
56,3384 |
1,16 |
288,738 |
206,477 |
1,398 |
66353,3 |
50614,2 |
1,31 |
|
64,1286 |
54,5542 |
1,17 |
274,403 |
199,22 |
1,377 |
62915,3 |
49397 |
1,27 |
|
64,7811 |
52,8636 |
1,22 |
279,28 |
186,225 |
1,5 |
65123,9 |
44643,3 |
1,46 |
|
61,6578 |
52,5726 |
1,17 |
259,311 |
182,213 |
1,42 |
59511,2 |
43948 |
1,35 |
|
61,5405 |
52,406 |
1,17 |
257,997 |
181,627 |
1,42 |
60545,9 |
44440,4 |
1,36 |
|
62,5105 |
52,6686 |
1,186 |
261,703 |
180,711 |
1,45 |
60253,1 |
43657,4 |
1,38 |
|
67,1808 |
51,7558 |
1,298 |
274,691 |
178,603 |
1,54 |
63829,7 |
43114, |
1,48 |
|
62,2612 |
51,0573 |
1,219 |
262,538 |
180,066 |
1,46 |
61498,6 |
43269,5 |
1,42 |
|
······················································································································ |
||||||||
|
57,3447 |
48,7582 |
1,18 |
213,986 |
146,001 |
1,47 |
51683,9 |
35685,9 |
1,45 |
|
58,2758 |
49,1556 |
1,19 |
217,216 |
145,298 |
1,49 |
48712,5 |
35111,6 |
1,39 |
|
59,1704 |
49,9447 |
1,18 |
221,598 |
149,191 |
1,48 |
50198 |
35754,8 |
1,4 |
|
59,754 |
50,4453 |
1,18 |
222,59 |
147,622 |
1,5 |
50463,4 |
36043 |
1,4 |
|
59,5839 |
50,6945 |
1,17 |
226,682 |
152,097 |
1,49 |
51125,3 |
37085,5 |
1,37 |
|
59,9658 |
50,2361 |
1,19 |
239,723 |
160,286 |
1,49 |
52170,9 |
38830,6 |
1,34 |
|
60,1732 |
49,6141 |
1,21 |
236,056 |
153,398 |
1,53 |
54281,2 |
36877,3 |
1,47 |
|
58,7683 |
48,5904 |
1,21 |
224,794 |
147,337 |
1,52 |
51029,5 |
35267,8 |
1,44 |
|
58,7425 |
47,7794 |
1,23 |
235,351 |
150,679 |
1,56 |
54115,9 |
35652,2 |
1,52 |
|
58,6477 |
46,0753 |
1,27 |
235,979 |
147,904 |
1,59 |
53861,8 |
36254 |
1,48 |
|
65,2978 |
47,9116 |
1,36 |
269,674 |
157,267 |
1,71 |
61929,2 |
38639,3 |
1,6 |
|
61,1794 |
50,4459 |
1,21 |
245,904 |
169,863 |
1,44 |
57297,3 |
40278,3 |
1,42 |
|
67,5181 |
51,62 |
1,307 |
267,603 |
177,462 |
1,51 |
62600,4 |
44058,6 |
1,42 |
|
65,956 |
52,4256 |
1,26 |
275,007 |
186,955 |
1,47 |
63581,3 |
45815 |
1,39 |
|
65,4575 |
51,4629 |
1,27 |
280,843 |
185,44 |
1,51 |
65229,5 |
44697,8 |
1,46 |
|
63,0209 |
53,0135 |
1,19 |
266,557 |
183,174 |
1,45 |
62154,6 |
44328,7 |
1,40 |
По полученным результатам можно увидеть, что отношения периметра, площади и объема полутени к периметру, площади и объему тени солнечного пятна практически являются постоянной величиной, что не противоречит результатам рассмотренных ранее работ [2, 3]. На рис. 3 представлена 3D модель солнечного пятна, полученная с помощью программы 3DFieldPro.
Использование математического пакета Matlab дает возможность проводить анализ временных рядов с помощью Фурье и вейвлет-анализов. Исследование функций во временных и частотных интервалах с помощью прямого Фурье-преобразования и обратного Фурье-преобразования составляет основу Фурье-анализа. Они показали, что для функций с локальными особенностями представление сигналов в виде ряда Фурье оказывается малоэффективным, в частности как для импульсных, так и для цифровых сигналов и изображений [4]. Представим наши результаты по вейвлет-анализу, основываясь на вышесказанном.
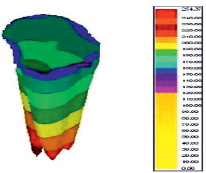
Рис. 3. 3D модель солнечного пятна
Вейвлеты [5] можно охарактеризовать следующими образами: временными и частотными. Временной образ – некоторая y(t) функция времени, а частотный образ – Фурье-образ 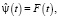 который задает огибающую вейвлет-спектра. Фурье-образ можно представить следующим выражением:
который задает огибающую вейвлет-спектра. Фурье-образ можно представить следующим выражением:
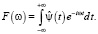
Рассмотрим вейвлет в пространстве: при его сужении «средняя» частота повышается, что приводит к перемещению спектра в области с более высокими частотами, т.е. к его расширению. Такие процессы можно отнести к линейным.
Вейвлет-преобразование и Фурье-преобразование отличаются в следующем: каждому вейвлету соответствует свое преобразование, т.е. оно определено неоднозначно. Если ω = 0, то Фурье-образ 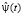 вейвлета равняется 0.
вейвлета равняется 0.
При прямом вейвлет-преобразовании происходит разложение произвольного входного сигнала на новый базис в виде совокупности так называемых волновых пакетов.
Получается, что вейвлет-спектрограммы становятся наиболее пригодными для анализа тонкой структуры сигналов, содержащих ярко выраженные скачки, всплески и переходы производных через ноль и так далее. К таким сигналам можно отнести: звуковые сигналы речи и музыки, а также сигналы изображений. Все это мы учитывали при составлении программы в математическом пакете Matlab.
Нами были обработаны более 60 пятен, наблюдавшихся на Солнце в разное время. Также был проведен вейвлет-анализ для длин изолинии пятна, площади и объема. На рис. 4–6 представлены некоторые результаты нашего исследования.
Параметры тени и полутени солнечного пятна
|
Lп – длина изолинии полутени |
Lт – длина изолинии тени |
Lп/Lт |
Sп – площадь полутени |
Sт – площадь тени |
Sп/Sт |
Vп – объем полутени |
Vт – объем тени |
Vп/Vт |
|
65,3882 |
54,3502 |
1,2 |
286,746 |
197,186 |
1,45 |
67029,7 |
48206,3 |
1,39 |
|
66,6326 |
54,3502 |
1,2 |
296,262 |
197,186 |
1,5 |
68235,8 |
48206,3 |
1,41 |
|
65,3702 |
56,3384 |
1,16 |
288,738 |
206,477 |
1,398 |
66353,3 |
50614,2 |
1,31 |
|
64,1286 |
54,5542 |
1,17 |
274,403 |
199,22 |
1,377 |
62915,3 |
49397 |
1,27 |
|
64,7811 |
52,8636 |
1,22 |
279,28 |
186,225 |
1,5 |
65123,9 |
44643,3 |
1,46 |
|
61,6578 |
52,5726 |
1,17 |
259,311 |
182,213 |
1,42 |
59511,2 |
43948 |
1,35 |
|
61,5405 |
52,406 |
1,17 |
257,997 |
181,627 |
1,42 |
60545,9 |
44440,4 |
1,36 |
|
62,5105 |
52,6686 |
1,186 |
261,703 |
180,711 |
1,45 |
60253,1 |
43657,4 |
1,38 |
|
67,1808 |
51,7558 |
1,298 |
274,691 |
178,603 |
1,54 |
63829,7 |
43114, |
1,48 |
|
62,2612 |
51,0573 |
1,219 |
262,538 |
180,066 |
1,46 |
61498,6 |
43269,5 |
1,42 |
|
······················································································································ |
||||||||
|
57,3447 |
48,7582 |
1,18 |
213,986 |
146,001 |
1,47 |
51683,9 |
35685,9 |
1,45 |
|
58,2758 |
49,1556 |
1,19 |
217,216 |
145,298 |
1,49 |
48712,5 |
35111,6 |
1,39 |
|
59,1704 |
49,9447 |
1,18 |
221,598 |
149,191 |
1,48 |
50198 |
35754,8 |
1,4 |
|
59,754 |
50,4453 |
1,18 |
222,59 |
147,622 |
1,5 |
50463,4 |
36043 |
1,4 |
|
59,5839 |
50,6945 |
1,17 |
226,682 |
152,097 |
1,49 |
51125,3 |
37085,5 |
1,37 |
|
59,9658 |
50,2361 |
1,19 |
239,723 |
160,286 |
1,49 |
52170,9 |
38830,6 |
1,34 |
|
60,1732 |
49,6141 |
1,21 |
236,056 |
153,398 |
1,53 |
54281,2 |
36877,3 |
1,47 |
|
58,7683 |
48,5904 |
1,21 |
224,794 |
147,337 |
1,52 |
51029,5 |
35267,8 |
1,44 |
|
58,7425 |
47,7794 |
1,23 |
235,351 |
150,679 |
1,56 |
54115,9 |
35652,2 |
1,52 |
|
58,6477 |
46,0753 |
1,27 |
235,979 |
147,904 |
1,59 |
53861,8 |
36254 |
1,48 |
|
65,2978 |
47,9116 |
1,36 |
269,674 |
157,267 |
1,71 |
61929,2 |
38639,3 |
1,6 |
|
61,1794 |
50,4459 |
1,21 |
245,904 |
169,863 |
1,44 |
57297,3 |
40278,3 |
1,42 |
|
67,5181 |
51,62 |
1,307 |
267,603 |
177,462 |
1,51 |
62600,4 |
44058,6 |
1,42 |
|
65,956 |
52,4256 |
1,26 |
275,007 |
186,955 |
1,47 |
63581,3 |
45815 |
1,39 |
|
65,4575 |
51,4629 |
1,27 |
280,843 |
185,44 |
1,51 |
65229,5 |
44697,8 |
1,46 |
|
63,0209 |
53,0135 |
1,19 |
266,557 |
183,174 |
1,45 |
62154,6 |
44328,7 |
1,40 |
Выводы
В данной статье проведена визуализация информации, полученной в результате наблюдений солнечных пятен, которые являются активными образованиями. Получены трехмерные модели солнечных пятен, данные модели показывают зависимость пятна от глубины и изменения температуры с глубиной. Все это выполнялось с помощью программы 3DField Pro.
Также мы провели вейвлет-анализ временных рядов, составлена программа в математическом пакете Matlab для выявления периодических составляющих сигнала.
Библиографическая ссылка
Джимбеева Л.Н., Бембитов Д.Б., Манкаева Г.А., Утнасунова В.О., Джимбеева А.О. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ СОЛНЕЧНЫХ ПЯТЕН // Научное обозрение. Технические науки. 2019. № 1. С. 10-14;URL: https://science-engineering.ru/ru/article/view?id=1224 (дата обращения: 03.03.2026).


 science-review.ru
science-review.ru