science-review.ru
Рассматривается классическая задача анализа устойчивости положения равновесия нелинейных гомогенных многосвязных систем, которые в каждом канале содержат нелинейность, расположенную в заданном угле.
Известна постановка и решение задачи [1] абсолютной устойчивости положения равновесия нелинейной системы с одним входом и одним выходом, у которой нелинейность расположена в заданном угле. Решение данной задачи осуществляется на основе подхода к проектированию сложных систем на основе описания МСАУ через характеристики подсистем и многомерные элементы связи между ними [2–4].
В данной статье рассматривается решение данной задачи для класса нелинейных гомогенных многосвязных систем автоматического управления.
Цель исследования: определить достаточное условие абсолютной устойчивости нелинейной многосвязной системы управления, основанное на системном описании МСАУ через характеристики связей и характеристики подсистем
Для описания системы используются методы теории управления, а именно: частотные методы; методы теории функций действительного и комплексного переменного и функционального анализа; методы системного анализа; основы матричного исчисления; методы теории множеств; методы линейной алгебры; методы имитационного и математического моделирования.
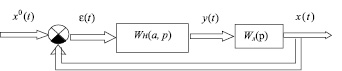
Рис. 1. Структурная схема нелинейной МСАУ
Пусть имеется нелинейная гомогенная многосвязная система (рис. 1) с несвязными регуляторами, при условии, что x0(t) = 0, описываемая следующими операторными уравнениями:
X(p) = Wн(а, p)Wл(p)E(p), (1)
где p – оператор дифференцирования.
Идентичные нелинейности находятся только в прямых каналах связи, а перекрестные связи между подсистемами являются голономными. Нелинейности (рис. 2) представляют собой однозначные статические характеристики произвольного вида, удовлетворяющие условию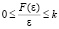 
.
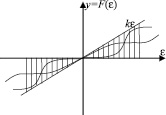
Рис. 2. Характеристики нелинейностей МСАУ
Все линейные звенья подсистем в разомкнутом состоянии объединены в линейную часть с передаточной функцией Wл(p). Будем также предполагать, что линейные части подсистем устойчивые и порядок их астатизма не превышает двух.
Введем следующие обозначения:
Фi(а,p) =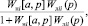 
(2)
Фi(а,p) – передаточная функция i-й сепаратной подсистемы в режиме управления.
Для гомогенных систем динамические характеристики локальных подсистем идентичны:
Ф1[a,p] = Ф2[a, p] =…= Ф[a, p].
Характеристическое уравнение нелинейной гомогенной МСАУ:
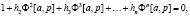(3)
где характеристика многомерной связи hi равна
,
, 
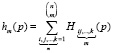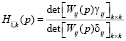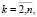
где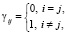 
,
.
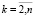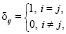
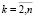Рассмотрим следующую задачу: требуется определить условия абсолютной устойчивости положения равновесия нелинейной гомогенной многосвязной системы.
Анализ абсолютной устойчивости
С учетом (3) введем в рассмотрение алгебраическое уравнение связи относительно переменной x следующего вида:
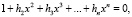(4)
где Ф[a, p] = x, а {xi} – множество корней уравнения связи, где i = 1,2 ..n.
Условием наличия в нелинейной многосвязной системе периодических движений является прохождение локальной амплитудно-фазовой частотной характеристики (АФХ) Ф(a,jw) подсистемы через одно из значений множества корней {xi} уравнения (4), играющих роль критических точек [5, 6].
В этом случае справедливо равенство
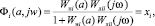(5)
где xi = ai ± jb, i = 1,2 ..n.
Выделим линейные и нелинейные характеристики разомкнутой подсистемы из уравнения (5):
Wн(a)Wл(jw)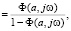
(6)
где Wл(jw)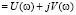
, а коэффициент передачи нелинейного элемента возьмем предельным из диапазона 
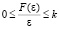, т.е. Wн(a) = k.
Подставляя xi вместо Ф(а,jw) в уравнение (6), получим
Wн(a)Wл(jw) =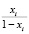 
= ci + jdi
или
kWл(jw) =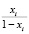 
= ci + jdi.
Откуда получаем условие, при котором нелинейная многосвязная система находится на границе устойчивости
Wл(jw) =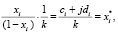 
i = 1,2 ..n, (7)
где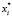 
– назовем модифицированным корнем.
Следовательно, корректна формулировка критерия абсолютной устойчивости МСАУ в следующем виде.
Если гомогенная многосвязная система состоит из подсистем, устойчивых или нейтральных в разомкнутом состоянии и содержащих нелинейные элементы с характеристиками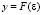 
, лежащими в диапазоне 
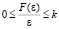, то для абсолютной устойчивости положения равновесия этой системы достаточно, чтобы АФХ Wл(jw) не охватывала ни один из модифицированных корней 
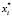, i =1,2 ..n (рис. 3).
Таким образом, анализ абсолютной устойчивости положения равновесия нелинейной гомогенной многосвязной системы состоит из следующих этапов:
1) определение линейных характеристик разомкнутых подсистем Wл(jw);
2) определение диапазона нелинейных характеристик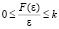 
;
3) нахождение корней характеристического уравнения связи xi;
4) вычисление модифицированных корней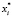 
, i = 1,2 n;
5) построение на комплексной плоскости годографа Wл(jw) и модифицированных корней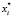 
, i = 1,2 ..n;
6) оценка абсолютной устойчивости положения равновесия нелинейной гомогенной многосвязной системы по частотному критерию.
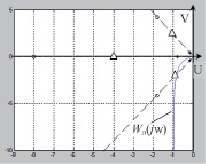
Рис. 3. Расположение относительно годографа модифицированных корней: ? – устойчивой системы; * – неустойчивой системы; ? – на границе устойчивости
Зная АФХ Wл(jw) подсистем, из соотношения (7) можно получить предельное значение k для диапазона, в котором могут располагаться нелинейные характеристики произвольной формы:
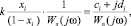i = 1,2 ..n. (8)
Это можно сделать в следующем порядке:
– определить линейные характеристики разомкнутых подсистем Wл(jw);
– построить на комплексной плоскости относительно параметра k кривые D-разбиения для каждого модифицированного корня, при i = 1, 2 ..n.
– определить устойчивую область по k и вещественные значения k, при которых нелинейная гомогенная многосвязная система будет устойчива.
Пример анализа влияния параметров системы управления на абсолютную устойчивость
Определить предельное значение k для диапазона, в котором могут располагаться нелинейные характеристики, при которых у трехсвязной системы (рис. 1) будет абсолютно устойчивое положение равновесия.
Передаточная функция объекта имеет вид
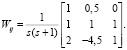
1. Передаточные функции Фi(a,p), i = 1,2,3 сепаратных каналов в режиме управления
Фi(a,p) =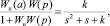 
(9)
где Wнi(a) = k, i = 1,2,3.
2. Находим корни характеристического уравнения связи xi. Характеристическое уравнение имеет вид
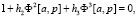
где h2 = 4, h3 = 1.
Корни характеристического уравнения связи 1 + 4х2 + х3 = 0 равны x1 = –4,06 x2,3 = 0,03 ± j0,5.
3. Выделим линейные и нелинейные характеристики разомкнутой подсистемы из уравнения (9) и вычислим значения Ki(jw) для каждого корня характеристического уравнения:
Wл(jw)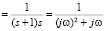
;
,
,
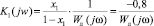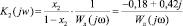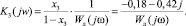
4. Построим кривые D-разбиения Ki(jw), i =1, 2, 3 на комплексной плоскости (рис. 4).
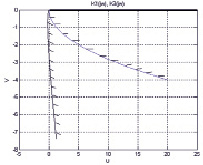
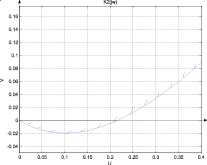
а) б)
Рис. 4. Значения k при различных корнях характеристического уравнения: а) 0 ≤ k ≤ +∞; б) 0 ≤ k ≤ 0,22
Важными являются только вещественные значения k. Значения k при различных корнях характеристического уравнения будут располагаться в следующем диапазоне:
0 ≤ k1 ≤ +∞; 0 ≤ k2 ≤ 0,22; 0 ≤ k3 ≤ +∞.
Из всех полученных значений выбирается минимальная область вещественных значений 0 ≤ k ≤ 0,22. Это значения k, при которых нелинейная трехсвязная система с нелинейными характеристиками произвольного вида, лежащими в диапазоне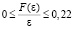 
будет устойчивой.
Пусть нелинейная характеристика находится в диапазоне 0 ≤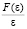 
≤ 1, т.е. k =1 лежит за пределами диапазона 0 ≤ k ≤ 0,22. В этом случае положение равновесия системы неустойчивое (рис. 5).
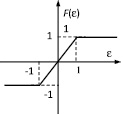
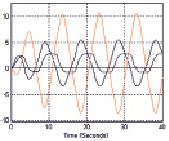
Рис. 5. Вид нелинейности и переходные процессы при k = 1
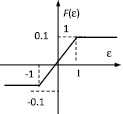
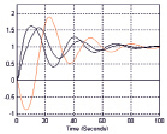
Рис. 6. Вид нелинейности и переходные процессы при k =0,1
Если нелинейная характеристика находится в диапазоне 0 ≤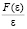 
≤ 0,1, т.е. k = 0,1 лежит в диапазоне 0 ≤ k ≤ 0,22, то положение равновесия системы устойчивое, что подтверждается результатами моделирования (рис. 6).
Заключение
Таким образом, предложенный частотный критерий дает достаточное условие абсолютной устойчивости положения равновесия нелинейной гомогенной многосвязной системы автоматического управления.
Работа выполнена при поддержке грантов РФФИ № 18-08-00702 А «Развитие методов анализа устойчивости многосвязных динамических систем управления сложными техническими объектами», № 18-08-01299 А «Проектирование интеллектуальных многосвязных систем управления статически неустойчивыми автономными подвижными объектами на основе методов нелинейной динамики, машинного обучения и искусственных нейронных сетей».
Библиографическая ссылка
Ильясов Б.Г., Саитова Г.А., Халикова Е.А. ДОСТАТОЧНОЕ УСЛОВИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ МНОГОСВЯЗНЫХ СИСТЕМ УПРАВЛЕНИЯ С ОДНОТИПНЫМИ ПОДСИСТЕМАМИ // Научное обозрение. Технические науки. – 2019. – № 1. – С. 27-31;URL: https://science-engineering.ru/ru/article/view?id=1227 (дата обращения: 03.12.2024).