science-review.ru
Граф знаний – это мультиреляционный граф, состоящий из сущностей, которые могут быть представлены как в виде связки узлов и отношений, так и в виде разнотипных ребер. В качестве экземпляра ребра может быть представлена тройка параметров (голова, отношение, хвост), она обозначается как (h, r, t) от англ. (head, relation, tail).
Наиболее важные варианты использования графов знаний в объединении с ИИ включают в себя [1]:
- интуитивно понятный поиск с использованием естественного языка;
- обнаружение соответствующего контента и информации в структурированных или неструктурированных данных;
- надежный контент и управление данными;
- прогнозирование операционного риска; и т.п.
Цель исследования: рассмотреть модели со скрытым расстоянием, используемые для реализации графа знаний. Сравнить обучаемые модели и выделить особенности каждой из них.
Объект исследования
Одними из алгоритмов реализации графа знания являются модели со скрытым расстоянием. Данные модели используют функции рейтинговой оценки, основанные на расстоянии между сущностями, для моделирования тройки графа знаний. Взаимодействие сущностей и отношений осуществляется через их скрытое пространственное представление.
TransE. TransE (от англ. Translating Embeddings for Modeling Multi-relational Data – Транслирование внедряемых сущностей в векторном пространстве для моделирования мультиреляционных данных) – это модель, основанная на EBM (от англ. Energy-Based Model), которая представляет отношения в виде трансляций в векторном пространстве. В частности, предполагается, что если триплет (h, r, t) имеет место, то внедрение сущности хвоста «t» должно быть близко к внедрению головной сущности «h» плюс некоторый вектор, который зависит от отношения «r». В TransE и сущности, и отношения являются векторами в одном и том же пространстве. Чтобы изучить такие внедрения, следует на обучаемой выборке минимизировать критерий ранжирования, основанный на границе ϒ [2]:
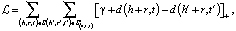
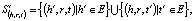
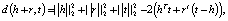
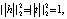
где []+ – представляет собой только положительную часть,
ϒ – граница, разделяющая положительные и отрицательные тройки,
d – функция расстояния,
S – множество положительных триплетов (h, r, t),
S' – множество отрицательных триплетов,
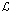– обучаемая модель,
E – множество сущностей, h, t ∈E.
TransH. TransH (от англ. Knowledge Graph Embedding by Translating on Hyperplanes – внедрение сущностей графа знаний путем транслирования на гиперплоскости) следует общему принципу TransE. Однако, по сравнению с ним, он вводит конкретные для отношений гиперплоскости. Сущности представлены в виде векторов, как и в TransE, однако отношение моделируется как вектор на собственной гиперплоскости с вектором нормали (рис. 1).
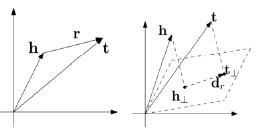
а) TransE б) TransH
Рис. 1. Иллюстрация алгоритмов моделирования графа знаний
Затем сущности проецируются на гиперплоскость отношения для расчета потерь. Чтобы стимулировать различие между хорошими триплетами и неправильными триплетами, используется следующий предельный рейтинг потери [3]:
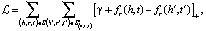
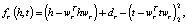
где wr – гиперплоскость для отношения r,
fr – функция оценки.
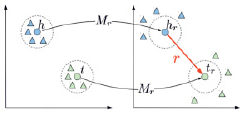
TransR. TransR (от англ. Relation Embeddings for Knowledge Graph Completion – внедрение отношений для заполнения графа знаний) очень похож на TransH, с той лишь разницей, что вместо того, чтобы иметь одну гиперплоскость отношения, он вводит множество гиперплоскостей (рис. 2).
Пространство сущностей Пространство отношений
Рис. 2. Иллюстрация алгоритма TransR
Сущности являются векторами в пространстве сущностей, и каждое отношение является вектором в определенном пространстве отношения. Для расчета потерь сущности проецируются в отношении конкретного пространства с использованием матрицы проекции. Для каждой тройки (h, r, t) сущности в пространстве сущностей сначала проецируются в пространство r-отношений hr и tr с помощью операции Mr, а затем приводят к уравнению вида hr + r ≈ tr [4].
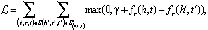
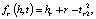
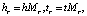
TransD. TransD (от англ. Knowledge Graph Embedding via Dynamic Mapping Matrix – внедрение сущностей графа знаний с помощью матрицы динамического отображения) – улучшенная версия TransR. Для каждого триплета (h, r, t) используются две матрицы отображения Mrh, Mrt∈Rmn для проецирования сущностей из пространства сущностей в пространство отношений. Mrh, Mrt сопоставляют матрицы h, t соответственно (рис. 3) [5].
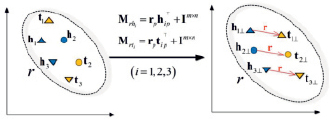
Пространство сущностей Пространство отношений
Рис. 3. Иллюстрация алгоритма TransD
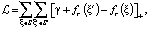
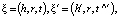
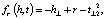
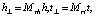
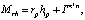
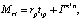
где р – вектор проекции,
Mrh, Mrt – матрицы динамического отображения,
Im*n – единичная матрица размером m×n.
TransM. TransM (от англ. Transition-based Knowledge Graph Embedding with Relational Mapping Properties – внедрение отношений для построения графа знаний на основе переходов со свойствами реляционного отображения) помогает устранить отсутствие гибкости алгоритма в TransE, когда дело доходит до сопоставления свойств триплетов. На рис. 4 продемонстрирована разница между алгоритмами. Используется структура графа знаний посредством предварительного вычисления индивидуального веса для каждого тестового триплета в соответствии с его свойством реляционного отображения. Простой способ смоделировать структуру – связать каждый тестовый триплет с весом, который представляет степень отображения. Согласно наблюдениям, свойство отображения триплета во многом зависит от его отношений внутри графа [6].
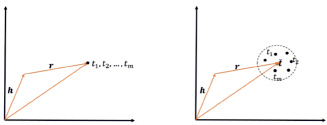
а) TransE б) TransM
Рис. 4. Различия между алгоритмами при моделировании экземпляров отношения один ко многим
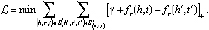
KG2E. KG2E (от англ. Knowledge Graphs with Gaussian Embedding – графы знаний с внедрением распределения Гаусса) вместо того, чтобы представлять сущности и отношения в качестве детерминированных точек в векторном пространстве, моделирует сущности и отношения (h, r, t), используя случайные величины, полученные из многомерного Гауссовского распределения. Затем KG2E оценивает события, используя отношение трансляций, оценивая расстояние между двумя распределениями r и t-h. KG2E предоставляет на выбор две меры расстояния (расстояние Кульбака – Лейблера и оценочная вероятность) [7].
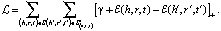
Расстояние Кульбака – Лейблера
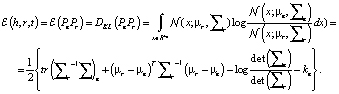
Оценочная вероятность
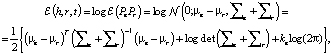
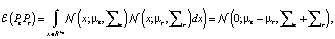
где tr(∑r) – трассировка ковариационной матрицы,
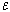– множество сущностей триплета,
DKL – расстояние Кульбака – Лейблера,
∑e, ∑r – ковариационные матрицы,
μ – вектор средних,
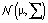– многомерное Гауссово распределение (с диагональной ковариацией для эффективности вычислений),
Pe, Pr – распределение вероятностей и отношений соответственно,
ke – размер сущности в скрытом векторном пространстве,
det – определитель матрицы.
Заключение
В заключение можно выделить основные характеристики описанных алгоритмов реализации графа знаний. При максимуме внимания на минимальной параметризации модели был разработан алгоритм TransE, чтобы в первую очередь представлять иерархические отношения. Он является хорошо масштабируемой моделью. TransH преодолевает недостатки TransE, связанные с рефлексивными отношениями «один ко многим / многие к одному / многие ко многим», при этом наследуя его эффективность. Обширные эксперименты классификации триплетов и извлечения реляционных сущностей показывают, что TransH приносит многообещающие улучшения в TransE. TransR предлагает внедрения посредством трансляции между проецируемыми сущностями. TransD имеет меньшую сложность и большую гибкость, чем TransR / CTransR. Обширные эксперименты показывают, что TransD превосходит TrasnE, TransH и TransR / CTransR по двум задачам, а именно классификации триплетов и прогнозированию ссылок. TransM – превосходная модель, которая не только идеальна для представления иерархических и нерефлексивных характеристик, но также гибкая для адаптации различных свойств отображения триплетов знаний. Результаты обширных экспериментов с несколькими эталонными наборами данных доказывают, что модель может достичь более высокой производительности без ущерба для эффективности. KG2E представляет собой новый метод для представлений сущностей и отношений. Обширные эксперименты по прогнозированию ссылок и классификации триплетов с несколькими наборами эталонных данных (включая WordNet и Freebase) демонстрируют, что предлагаемый метод превосходит аналоговые методы.
Библиографическая ссылка
Хлопенкова А.Ю., Белов Ю.С. ИССЛЕДОВАНИЕ МОДЕЛЕЙ СО СКРЫТЫМ РАССТОЯНИЕМ ДЛЯ ВНЕДРЕНИЯ СУЩНОСТЕЙ И ИХ ОТНОШЕНИЙ В ГРАФ ЗНАНИЙ // Научное обозрение. Технические науки. – 2020. – № 5. – С. 38-42;URL: https://science-engineering.ru/ru/article/view?id=1314 (дата обращения: 23.11.2024).