Для гиперупругих материалов (неорганических и органических) закон Гука не выполняется [1, 2], и для описания деформационных свойств требуется применение различных нелинейных моделей, при этом выбор модели, которая была бы адекватной опытным данным, представляет актуальную задачу механики [3]. С точки зрения медицины оценка этих параметров может служить диагностическим показателем состояния биотканей, а знание характеристик их деформационных свойств может быть применено при реконструктивных вмешательствах и разработке замещающих искусственных аналогов– эндопротезов. Хорошо известна также востребованность гиперупругих моделей деформирования при проектировании изделий технического назначения с использованием так называемых эластомерных материалов.
Целью исследования было систематизировать рабочие формулы F(λ) для расчета гиперупругих моделей и представить основные фрагменты алгоритмов вычислений параметров моделей в пакете Mathcad.
Материалы и методы исследования
Расчет параметров гиперупругих моделей [4–6] производили в системе компьютерной алгебры Mathcad 15.0 (PTC Inc., США). Результаты расчетов верифицировались с помощью параллельных вычислений в многофункциональном пакете ANSYS 2022 R2.
В качестве примера рассмотрен биоматериал– ткани ногтевой пластины человека. Исходные данные пластины были представлены кривыми напряжение– деформация σ-ε [7]. Для удобства размещения в тексте статьи они представлены векторами (матрицами) в транспонированном и сокращенном виде:
,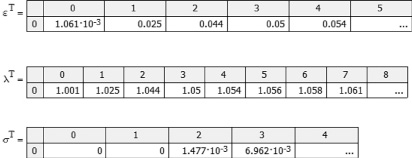
где σ– инженерные (условные) напряжения, [σ] = ГПа.
Результаты исследования и их обсуждение
Неогуковская модель
Алгоритм расчета основан на применении функции «подгонки» linfit– функции аппроксимации по методу наименьших квадратов (она возвращает вектор с параметрами, которые используются для создания линейной комбинации функций):
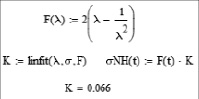
где K– это материальная константа μ неогуковской модели (ГПа).
Модель Муни– Ривлина (2-параметрическая)

где строки в столбце (компоненты вектора)– постоянные модели C10 и C01 (ГПа).
Модель Муни– Ривлина (3-параметрическая)

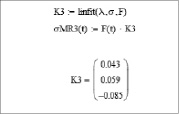
где строки в столбце (компоненты вектора)– постоянные C10, C01 и C11.
Модель Муни– Ривлина (5-параметрическая)

где строки в столбце (компоненты вектора)– постоянные C10, C01, C11, C20 и C02.
Модель Йео
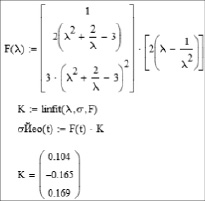
где строки в столбце (компоненты вектора)– постоянные C1, C2 и C3.
Модель Муни– Ривлина (9-параметрическая)
Самая многочисленная по числу параметров модель Муни– Ривлина.

где строки в столбце (компоненты вектора)– постоянные C10, C01, C11, C20, C02, C21, C12, C30 и C03.
Отметим, что 9-параметрическая модель рекомендована к применению для деформационных кривых, содержащих две и более точек перегиба.
Модель Огдена (1-го порядка)
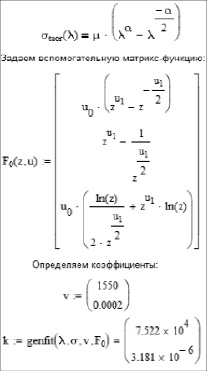
где строки в столбце (компоненты вектора)– постоянные μ и α.
Полиномиальная модель (2-го порядка)

где строки в столбце (компоненты вектора)– постоянные C10, C01, C11, C20 и C02.
Модель Веронда-Вестманн
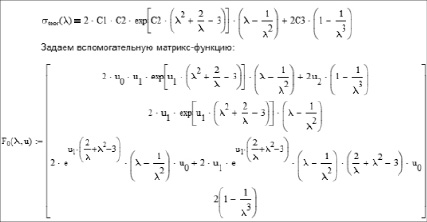

где строки в столбце (компоненты вектора)– постоянные C1, C2 и C3.
Близость экспериментальных и модельных данных и прогностические качества моделей оценивали с помощью показателей математической статистики: среднеквадратичного отклонения (СКО), максимального абсолютного отклонения (Δ), приведенной погрешности (δ, %) и коэффициента корреляции R:

В качестве примера расчета статистических показателей использованы данные 9-параметрической модели Муни– Ривлина ногтевой пластины человека.
Результаты вычислений параметров гиперупругих моделей представлены нарисунке.
Из графика, представленного на рисунке, наглядно видно, что полиномиальная модель имеет наилучшие показатели качества аппроксимации рассматриваемых экспериментальных данных ногтевой пластины, взятых для расчета.
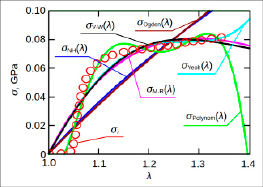
Сравнение рассмотренных прогностических гиперупругих моделей (сплошные линии): неогуковской (NH), 2-параметрической Муни– Ривлина (M-R), Огдена 1-го порядка (Ogden), Йео 3-го порядка (Yeoh), полиномиальной 2-го порядка (Polynom) и Веронда-Вестманн (V–W) и опытных данных (точками). Ногтевая пластина человека
Заключение
Таким образом, система Mathcad достаточно удобна и может быть рекомендована для расчета параметров гиперупругих моделей материалов. Относительная простота и точность, а также прозрачность вычислительных процедур выгодно выделяют ее среди других математических пакетов ANSYS, Comsol, MATLAB, MECHANICA и других, более рутинных, менее доступных и требующих специальной подготовки.
Библиографическая ссылка
Муслов С.А., Зайцева Н.В., Чистяков М.В., Фищенко К.А. MATHCAD АДАПТАЦИЯ ГИПЕРУПРУГИХ МОДЕЛЕЙ // Научное обозрение. Технические науки. 2024. № 2. С. 50-55;URL: https://science-engineering.ru/ru/article/view?id=1466 (дата обращения: 31.01.2026).
DOI: https://doi.org/10.17513/srts.1466


 science-review.ru
science-review.ru