science-review.ru
Введение
В оптике однородных сред, элементную базу которой составляют линзы со сферическими и асферическими поверхностями, выполненные из однородных оптических материалов, зеркала и дифракционные линзы (ДЛ), параметром, достаточным для характеристики каждого из оптических элементов при ахроматической коррекции оптической системы, является коэффициент дисперсии, известный как число Аббе [1].
Напомним, что ахроматическая коррекция направлена на достижение равенства оптических сил системы на двух крайних длинах волн рабочего спектрального диапазона. Число Аббе однородного оптического материала получают, используя значения показателя преломления на трех реперных длинах волн и в общем случае для диапазона волн от λshort до λlong оно описывается выражением
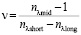, (1)
где индексы λmid, λshort и λlong относятся к центральной, короткой и длинной волнам (λshort ≤ λmid ≤ λlong) заданного диапазона.
Большинство оптических материалов обладают положительной (нормальной) дисперсией, при которой показатель преломления уменьшается с ростом длины волны.
Чтобы скорректировать вторичный спектр при апохроматической коррекции, направленной на достижение равенства оптических сил оптической системы на трех длинах волн рабочего спектрального диапазона, используется дополнительная характеристика, называемая частной дисперсией [1]. Частная дисперсия для определенного интервала длин волн от λi до λj имеет вид
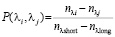, (2)
где λshort ≤ λi <λj ≤ λlong.
Если оптическая сила однородной линзы определяется показателем преломления ее материала, кривизнами рабочих поверхностей и толщиной, то в случае неоднородной линзы к этим параметрам добавляется градиент ее показателя преломления.
Сегодня наиболее распространенным типом среди неоднородных линз являются радиально-градиентные линзы (РГЛ). В общем случае закон изменения показателя преломления РГЛ описывается степенным рядом с базовым показателем преломления n0(λ) и коэффициентами радиального градиента ni(λ):
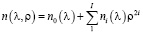, (3)
где λ и ρ – длина волны и расстояние от оптической оси.
Если на любой фиксированной длине волны показатель преломления n(λ,ρ) определяет вклад в оптическую силу и в составляющие сферической аберрации РГЛ, то зависимости базового показателя преломления и коэффициентов радиального градиента от длины волны определяют дисперсионные свойства неоднородного материала РГЛ.
В случае оптики неоднородных сред и при условии, что оптическая сила элемента определяется только его толщиной и градиентом показателя преломления, характеристика аналогичная числу Аббе имеет вид [2, 3]
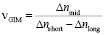, (4)
где Δnshort, Δnmid и Δnlong – изменение показателя преломления от центра к краю РГЛ на трех реперных длинах волн. Аналогично частная дисперсия может быть определена для неоднородного материала как [2, 3]
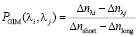. (5)
Стандартные дисперсии, описываемые уравнениями (1) и (2), и в оптике неоднородных сред используются при оценке хроматического приращения оптической силы, за которую отвечают, в частности, кривизны рабочих поверхностей линзы. В этом случае показатель преломления в указанных уравнениях относится к вершине поверхности. Отсюда следует, что РГЛ обладает двумя различными механизмами формирования как оптической силы, так и дисперсии.
Возможность независимого управления фокусирующими и дисперсионными свойствами РГЛ делает такой элемент наиболее универсальным и эффективным корректором одновременно как монохроматических, так и хроматических аберраций. Даже ближайшая к РГЛ ДЛ не может сравниться с ней коррекционными возможностями. Действительно у ДЛ оптическая сила и составляющие сферической аберрации на фиксированной длине волны легко управляются законом чередования кольцевых зон микроструктуры. При этом оптическая сила ДЛ на любой длине волны
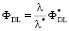, (6)
где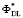 
– оптическая сила на расчетной длине волны λ*, на которой для заданной 
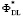рассчитывались радиусы кольцевых зон микроструктуры ДЛ.
Что касается первичного хроматизма ДЛ, то его, как и дисперсию однородного стекла, характеризуют коэффициентом дисперсии [4]. Он имеет вид
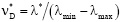. (7)
То есть коэффициент дисперсии от микроструктуры ДЛ не зависит, а следовательно, и не управляется, целиком определяясь шириной заданного спектрального диапазона.
Возвращаясь к РГЛ и принимая во внимание всю историю развития градиентной оптики, следует констатировать, что реальная возможность управления теми или иными свойствами градиентных оптических элементов зависит от технологии получения неоднородных материалов этих элементов.
Целью исследования является сопоставление возможностей управления фокусирующими и дисперсионными свойствами неоднородных материалов РГЛ видимого и инфракрасного (ИК) диапазонов в зависимости от представляющихся сегодня наиболее перспективными аддитивных технологий их изготовления: 3D-струйной печати с использованием нанокомпозитных оптических чернил и метода ламинирования, заключающегося во взаимной термической диффузии слоев при спекании многокомпонентной заготовки.
Материалы и методы исследования
Дисперсионные свойства материалов РГЛ видимого и ИК диапазонов, изготавливаемых 3D-струйной печатью и методом ламинирования. Теоретический анализ в рамках геометрической оптики.
Результаты исследования и их обсуждение
1. Возможности управления дисперсией нанокомпозитных РГЛ видимого диапазона
Фундаментальные свойства традиционно используемых оптических материалов и технологические проблемы до недавнего времени ограничивали возможность независимого управления оптическими свойствами синтезируемых неоднородных материалов, такими как показатель преломления и дисперсия. Создание пригодных для 3D-струйной печати нанокомпозитных материалов, получивших название «оптических чернил», различающихся концентрацией мономеров и нескольких нанонаполнителей, в сочетании с усовершенствованной технологией самой струйной печати сняло это ограничение и позволило независимо управлять градиентом показателя преломления и дисперсией формируемых неоднородных оптических материалов [5].
Сами нанокомпозитные чернила изготавливают путем внедрения в заданной концентрации в смесь фотоотверждающихся мономеров с низкой вязкостью одной или нескольких органических или неорганических наночастиц. Каждая наночастица имеет размер менее 10 нм, что составляет примерно 1/30 от самой короткой длины волны света, проходящего через оптическое устройство, и химически покрыта для устранения агломерации, так что рассеяние Рэлея и Ми незначительно [6]. Кроме того, чернила обладают реологическими свойствами, необходимыми для точной печати [7].
Формула (3), описывающая закон изменения показателя преломления РГЛ, не может непосредственно использоваться для оптимизации оптического материала этой линзы. Во-первых, коэффициенты радиального градиента, входящие в эту формулу, не отражают композитного характера неоднородного оптического материала. Во-вторых, коэффициенты n0(λ) и ni(λ) зависят от длины волны, и хроматическая дисперсия каждого коэффициента различна. Она является функцией как дисперсий компонентов композитного материала, так и соотношения их концентраций. Поэтому закон изменения показателя преломления РГЛ следует выразить через показатели преломления компонентов композитного материала и через их концентрации. Это позволяет сделать описанная в работах [3, 5, 8] простая линейная модель бинарных (состоящих из двух компонентов) чернил. В соответствии с ней чернила плавно превращаются из одного компонента в другой путем изменения концентраций. В линейной модели показатель преломления композитного материала описывается как линейная комбинация показателей преломления его компонентов:
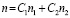, (8)
где n – показатель преломления композитного материала, n1 и n2 – показатели преломления первого и второго компонентов соответственно; C1 и C2 – доли первого и второго компонентов такие, что
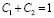. (9)
Величину Ci можно принять за объемную долю компонента i или считать относительной концентрацией компонента i. Поэтому уравнение (8) можно также записать как
.(10)
Ниже покажем, как коэффициенты радиального градиента РГЛ могут быть выражены через концентрации компонентов композитного материала.
Для исключения путаницы в обозначениях, следуя работе [3], закон изменения показателя преломления РГЛ перепишем в виде
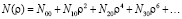. (11)
По форме таким же рядом можно записать распределение концентрации
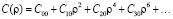. (12)
Комбинируя уравнения (11), (12) и (10), можно получить следующее соотношение для коэффициентов полинома распределения показателя преломления:
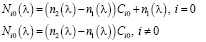. (13)
Линейная модель композитного материала является наиболее простой и дает удовлетворительный результат практически во всех случаях, поэтому она наиболее часто используется как для демонстрации хроматических свойств отдельных элементов, так и при расчете оптических систем с такими элементами [3, 8]. При этом линейное уравнение (8) не является идеальным приближением, также могут применяться квадратичная формула и формула Лоренца – Лоренца [3].
Действительно, двухкомпонентная линейная модель композитного материала предоставляет разработчику оптики инструменты для оценки числа Аббе νGIM и частной дисперсии PGIM любых как реально существующих, так и гипотетических неоднородных материалов. При известных значениях показателей преломления компонентов в конечных точках диапазонов их изменений и на реперных длинах волн νGIM и PGIM соответственно равны
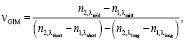(14)
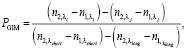(15)
где индексы λmid, λi, λj, λshort и λlong относятся к тем длинам волн, на которых зафиксированы показатели преломления первого и второго компонентов.
Технология 3D-струйной печати с использованием нанокомпозитных оптических чернил позволяет легко варьировать их дисперсионными характеристиками, подбирая концентрацию и число компонентов с высокими и низкими показателями преломления. Это и обеспечивает возможность независимого управления фокусирующими и дисперсионными свойствами изготавливаемых РГЛ.
Завершая раздел, приведем одно из реальных достижений в создании РГЛ струйной 3D-печатью. Это результаты работы компании NanoVox Optics [9], которая использует мономеры с высоким и низким показателями преломления, наполненные наночастицами. Компания изготовила машину для опытного производства, способную иметь до восьми печатающих головок с особыми чернилами в каждой. Эта система третьего поколения регулирует дозирование чернил, чтобы создавать оптику, в которой показатель преломления меняется с переходом от одного небольшого объема к другому.
Потенциальные области применения градиентной оптики, созданной по технологии струйной печати, включают, в частности, камеры мобильных телефонов. Благодаря РГЛ количество оптических элементов удается сократить с восьми-девяти до четырех. Еще одной областью применения может быть разработка очков виртуальной и дополненной реальности, где критически важно учитывать расстояние между глазами наблюдателя. 3D-печать позволяет осуществлять персонализацию быстро и в конечном счете без дополнительных затрат.
2. Возможности управления фокусирующими и дисперсионными свойствами РГЛ ИК-диапазона с ламинированным градиентным материалом
Вторая рассматриваемая здесь технология получения композитных градиентных материалов основана на методе ламинирования, заключающемся во взаимной термической диффузии слоев при спекании многокомпонентной заготовки. Под данную технологию разработана специальная серия новых марок халькогенидных стекол, прозрачных в широком диапазоне ИК-спектра (от 0,9 до 14 мкм). Показатель преломления этих стекол охватывает интервал от 2,38 до 3,17, и при этом они обладают близкими значениями температурных коэффициентов теплового расширения, а также совместимыми профилями вязкости [10–12].
Диапазон оптических характеристик и количество марок этих новых стекол позволяет с достаточной гибкостью варьировать значением градиента показателя преломления формируемого неоднородного материала. При этом параметры технологического процесса коаксиального ламинирования могут быть подобраны так, чтобы зависимость показателя преломления от расстояния от оптической оси РГЛ описывалась гладкой функцией и при этом на заданном расстоянии от оптической оси сохранялся неизменным показатель преломления стекла, используемого для данного слоя [13]. Важно также отметить, что халькогенидные стекла относятся к материалам, допускающим прецизионное прессование в качестве метода формообразования поверхности оптического элемента [14]. Это в совокупности с методом ламинирования открывает возможности создания градиентного материала для линз с оптимизированными под конкретное схемное решение оптическими свойствами.
Если закон изменения показателя преломления РГЛ, ограниченной асферическими или даже сферическими поверхностями, описывается формулой (3) при i ≥ 3 и при произвольном соотношении n1 и n0, то фокусирующие и дисперсионные свойства описываются громоздкими выражениями, трудно поддающимися анализу. В то же время, если на РГЛ накладываются ограничения, введенные в работе [3], это приводит к разделению параметров, а главное – к описанию фокусирующих и дисперсионных свойств относительно простыми аналитическими выражениями. Указанные ограничения предполагают у РГЛ параболический закон изменения показателя преломления
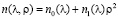, (16)
То есть n2 = n3 = 0 и малый аргумент синуса
. (17)
В этом случае оптическая сила РГЛ равна сумме сил однородной линзы φHL (с показателем преломления n0, осевой толщиной d, кривизнами преломляющих поверхностей c1, c2) и φGIM – радиально-градиентной плоскопараллельной пластины (шайбы) толщиной d:
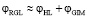, (18)
где
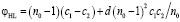; (19)
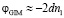. (20)
При этом общее изменение показателя от края элемента (ρ = ρmax) к его центру (ρ = 0), то есть к оптической оси, пропорционально n1:
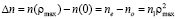, (21)
или
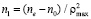. (22)
В (21) и (22)
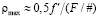, (23)
где f ' – фокусное расстояние оптической системы, в состав которой входит РГЛ, а F/# – ее диафрагменное число.
Оговоренные выше ограничения целесообразно дополнить соотношением, установленным авторами настоящей статьи на основе предшествующего опыта расчета ИК-объективов с РГЛ, показывающим, что оптимальные решения содержат, как правило, РГЛ, чья положительная составляющая оптической силы, обусловленная градиентом показателя преломления, составляет лишь небольшую (порядка одной двадцатой) часть от полной оптической силы этой линзы (φGIM/(φHL+φGIM) = 1/20). В результате нетрудно получить
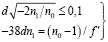. (24)
Система уравнений (24) позволяет подобрать оптические материалы, способные обеспечить на выбранной длине волны требуемый градиент показателя преломления РГЛ.
В соответствии с обобщенным определением числа Аббе [3]
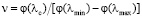(25)
и благодаря вышеприведенным ограничениям, формула для числа Аббе РГЛ, входящего в уравнения коррекции хроматизма, также принимает относительно простой вид
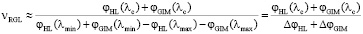, (26)
φ(λc), φ(λmin), φ(λmax) – оптическая сила на центральной, минимальной и максимальной длинах волн рабочего спектрального диапазона соответственно.
Учитывая, что в соответствии с (25) и (26) числа Аббе для однородной и градиентной составляющих оптических сил РГЛ равны
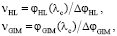(27)
и вводя коэффициент, равный отношению составляющий этих оптических сил,
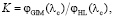(28)
для числа Аббе РГЛ нетрудно получить
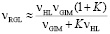. (29)
Далее, возвращаясь к формуле (26) и полагая, что одна из преломляющих поверхностей РГЛ плоская, то есть c1c2 = 0, для числа Аббе этой линзы получим
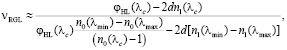(30)
или
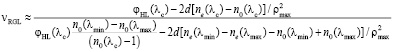. (31)
Формула числа Аббе, полученная аналогичным образом, но для РГЛ с двумя неплоскими преломляющими поверхностями (и, в частности, при с2 = –с1 и с1с2 = –с12), показала, что относительная погрешность, обусловленная переходом от плоско-выпуклой к двояко-выпуклой РГЛ, при аналитическом расчете числа Аббе во всех практически значимых случаях не превышает 1,5 %, а при лучевом расчете – 2 %.
Частная дисперсия РГЛ с учетом формул (2) и (31) описывается выражением
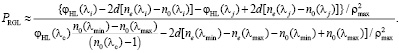(32)
Из формул (31) и (32), так же как и из формул (4) и (5), следует, что прямое воздействие на число Аббе и частную дисперсию рассматриваемой РГЛ законом распределения показателя преломления невозможно. Эти характеристики зависят от соотношения оптических сил однородной и градиентной составляющих оптической силы РГЛ K, а также дисперсионных свойств стекол, использованных для внутреннего цилиндрического стержня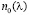 
и внешнего трубчатого слоя 
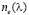ламинированного набора.
Завершая раздел, приведем два из опубликованных реальных достижений в области создания неоднородных материалов методом ламинирования. В работе [15] сообщалось о том, что разработана серия диффузионно совместимых халькогенидных стекол для изготовления градиентной оптики для сплошного ИК-диапазона от коротковолновой до длинноволновой области с перепадом показателя преломления Δn ≤ 0,4. Было продемонстрировано, что толщины слоев, допускающие диффузионное сглаживание кривой изменения показателя преломления могут достигать 1400 мкм. Кроме того, из разработанной серии халькогенидных стекол была изготовлена заготовка толщиной 3,5 мм с осевым приблизительно линейным распределением показателя преломления и его перепадом Δn ≈ 0,2.
Что касается неоднородных материалов с радиальным распределением показателя преломления, то в работе [12] сообщалось о разработке и отладке процесса, в ходе которого вместо плоских листов тонкие ИК-стеклянные трубки термически склеиваются и диффундируют. Достигнутый диаметр заготовки составляет 13,8 мм, а перепад показателя преломления Δn ≈ 0,2.
Заключение
Градиентная оптика, которой посвящена настоящая статья, имеет конкретную дату рождения. Это дата опубликования в 1854 г. Дж. Максвеллом первой работы, описывающей среду со сферически симметричным распределением показателя преломления, получившую название «рыбий глаз» и являющуюся абсолютным прибором, в котором отображение осуществляется преобразованием инверсии. За прошедшие более полутора веков ученые и специалисты многократно пытались использовать градиент показателя преломления для совершенствования оптических приборов. И каждый раз реализовать в полной мере найденные решения не удавалось из-за отсутствия требуемых оптических материалов и технологических ограничений.
Тезис, под которым возрождался интерес к градиентной оптике в 1980-е гг., утверждавший, что химические и физико-химические технологии окажутся эффективнее механической обработки оптических поверхностей, не оправдался. Появилось алмазное точение, специальные сорта стекол, допускающие прецизионную штамповку линз с асферическими поверхностями, и т.д.
Очень хочется надеяться, что созданные в последние годы аддитивные технологии получения неоднородных материалов с осевым, радиальным и сферическим распределениями показателя преломления вдохнут новую жизнь в градиентную оптику и окажутся коммерчески востребованными, что обеспечит финансовую базу ее дальнейшего развития.
Настоящая статья адресована широкому кругу читателей – от студентов соответствующих специальностей до разработчиков и производителей оптических приборов. Она знакомит читателя с возможностями, открывающимися в градиентной оптике видимого диапазона благодаря 3D-струйной печати, использующей нанокомпозитные оптические чернила, а также в градиентной оптике ИК-диапазона благодаря методу ламинирования, заключающемуся во взаимной термической диффузии слоев при спекании многокомпонентной заготовки.
Рассмотренные в данной работе технологии изготовления градиентных материалов демонстрируют реализуемость тех широких потенциальных возможностей простых по конструкции оптических систем, которые достигнуты благодаря расширению их элементной базы, в частности за счет градиентных элементов, и описаны в целом ряде статей, опубликованных за последние несколько лет.
Библиографическая ссылка
Грейсух Г.И., Левин И.А., Ежов Е.Г. ДИСПЕРСИЯ ОБЪЕМНЫХ СТРУЙНО-ПЕЧАТНЫХ И ЛАМИНИРОВАННЫХ МАТЕРИАЛОВ РАДИАЛЬНО-ГРАДИЕНТНЫХ ЛИНЗ // Научное обозрение. Технические науки. 2025. № 2. С. 5-11;URL: https://science-engineering.ru/ru/article/view?id=1496 (дата обращения: 19.05.2025).
DOI: https://doi.org/10.17513/srts.1496