Одной из наиболее часто встречающихся задач обработки изображений является задача определения опорных точек. Опорные точки – это некие точки на изображении, имеющие уникальные свойств, например точки:
1) с наибольшим градиентом в определенной области;
2) с наибольшей или наименьшей яркостью;
3) находящиеся в углах проходящих по изображению линий, и т.д.
В дальнейшем определенные точки используются в таких задачах, как навигация [1], склейка панорамных изображений [2], определение позы человека или его эмоций по лицу [3], создание дополненной реальности [4] и т.д.
Соответственно, каждый способ определения опорных точек обладает преимуществами, помогающими при решении той или иной задачи: инвариантность к освещению, повороту, изменению точки обзора и т.д.
Для однозначного определения опорных точек используются дескрипторы, которые в зависимости от метода могут являться векторами или матрицами значений, вычисляемыми для каждой опорной точки и указывающими на ее основные признаки.
В работе рассматриваются различные методы нахождения опорных точек на изображениях, а также оценены качество определения и производительность каждого метода с целью выявления наиболее точного метода с низкой вычислительной сложностью.
Материал и методы исследования
Для оценки методов использовался набор из 7366 изображений, созданных из фотографий местности, отснятых со спутника.

Рис. 1. Пример изображений
Такие изображения содержат большое количество мелких деталей и шума, что позволит проверить методы в более сложных условиях. Каждая пара изображений в наборе соответствует одному участку местности. На изображениях показан участок размером 1200×1200 метров, погрешность смещения изображений относительно друг друга составила 0,68 метра. Все изображения трехканальные, преобразованные к размеру 500×500 пикселей. Пример изображений приведен на рисунке 1. Как видно из примера, изображения были получены в разное время суток и года, отличаются также и настройки камеры при съемке, что приводит к различиям в цветовых пространствах изображений.
Для проведения тестирования использовались следующие методы определения опорных точек на изображениях:
1) SIFT (Scale Invariant Feature Transform) [5] – метод, использующий для определения опорных точек пирамиду изображений различных размеров, к которой применяется фильтр Гаусса. Опорные точки определяются как локальные максимумы на изображениях нескольких уровней увеличения при помощи разности гауссианов. В качестве определений используются гистограммы направлений градиентов, полученные в опорной точке и ее окрестностях, представленные в виде 128-мерной матрицы. Поскольку опорная точка является локальным максимумом, в окрестностях этой точки лежат участки с отличающимися градиентами, таким способом достигается инвариантность метода к повороту изображения. Использование пирамиды изображений также делает этот метод инвариантным к масштабированию;
2) FAST (Features from Accelerated Segment Test) [6] – эвристический метод, отличающийся высокой скоростью вычисления. Для определения опорной точки анализируются 4 точки, находящиеся на расстоянии в 3 пикселя от потенциальной опорной. Если как минимум 3 из них темнее или светлее опорной, проверяются все 16 точек, лежащие на таком же расстоянии от нее. Если из них 12 последовательных точек темнее или светлее, точка помечается как опорная;
3) BRIEF (Binary Robust Independent Elementary Features) [7] – быстрый метод определения дескрипторов опорных точек. Дескрипторы определяются с помощью бинарных сравнений яркостей пикселей между опорной точкой и 256 случайными точками в области 31×31 пиксель вокруг опорной. Полученные дескрипторы инвариантны к освещению и искажению перспективы, но неустойчивы к повороту;
4) AKAZE (Accelerated-KAZE) [8] – система из детектора и дескриптора, основанная, как и SIFT, на пирамиде изображений, однако масштаб увеличения пирамиды в данном случае нелинеен, что позволило увеличить скорость нахождения опорных точек. В отличие от SIFT, опорные точки определяются с помощью определителя Гессиана пикселей в окрестности потенциальной опорной точки. Дескриптор вычисляется похожим на BRIEF методом, но при этом учитываются и значения градиентов по осям, проходящим через опорную точку;
5) ORB (Oriented FAST and Rotated BRIEF) [9] – этот метод появился в результате развития и объединения методов FAST и BRIEF с целью уменьшения влияния поворота изображения на качество дескрипторов. Это было достигнуто путем вычисления поворота опорной точки и последующего поворота матрицы координат точек, использующихся при расчете BRIEF;
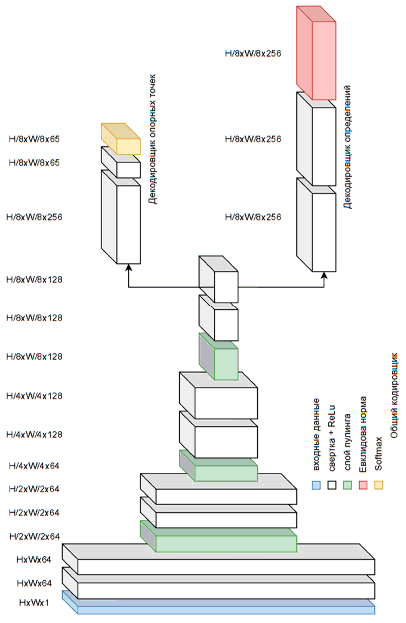
Рис. 2. Схема SuperPoint
6) SuperPoint [10] – самообучающаяся нейронная сеть, принимающая на вход одноканальное изображение любого размера. Сеть с помощью последовательного применения нескольких операций свертки кодирует изображение в набор особенностей, а далее декодирует эти особенности в два набора – опорных точек изображения и их дескрипторов (вектор из 256 чисел). Схема сети приведена на рисунке 2.
Соответственно, поскольку FAST определяет только положение опорных точек, а BRIEF – только их дескрипторы, эти два метода использовались в паре между собой.
Для сопоставления полученных опорных точек и их дескрипторов для ORB и FAST+BRIEF использовалось расстояние Хэмминга, для SIFT, AKAZE и SuperPoint – метрика L1. Количество определенных опорных точек для каждого метода ограничивалось 100. Качество определения определялось по числу сопоставленных опорных точек и среднему расстоянию между их координатами на разных изображениях.
Для сравнения производительности также было замерено среднее время определения и сопоставления опорных точек между двумя изображениями.
Результаты исследования и их обсуждение
Результат тестирования представлен в таблице 1. Для всех методов, кроме SuperPoint, изображения были представлены в двух вариантах – трехканальное цветное и одноканальное в градациях серого. Жирным шрифтом выделены наилучшие результаты – наибольшее число определенных точек и наименьшее расстояние между ними. Параметры методов были подобраны для получения наилучшего результата.
Также была определена производительность методов как среднее время определения и сопоставления 100 опорных точек по всему набору данных, результат представлен в таблице 2.
Далее, на рисунках 3–7, представлены результаты сопоставления точек на паре изображений, приведенной выше. Линиями соединены точки, определенные как похожие на изображениях.
Таблица 1
Результаты тестирования
|
Метод |
Число каналов изображения |
Количество совпадающих точек |
Среднее расстояние между точками |
|
FAST+BRIEF |
1 |
16.230 |
3.421 |
|
3 |
15.862 |
3.537 |
|
|
SIFT |
1 |
18.561 |
40.133 |
|
3 |
18.065 |
34.106 |
|
|
AKAZE |
1 |
19.658 |
35.102 |
|
3 |
20.184 |
38.862 |
|
|
ORB |
1 |
28.006 |
24.741 |
|
3 |
22.186 |
28.340 |
|
|
SuperPoint |
1 |
58.125 |
1.221 |
Таблица 2
Результаты замера производительности
|
Метод |
Число каналов изображения |
Средняя скорость выполнения, с |
|
FAST+BRIEF |
1 |
0.939 |
|
3 |
0.948 |
|
|
SIFT |
1 |
0.480 |
|
3 |
0.483 |
|
|
AKAZE |
1 |
0.129 |
|
3 |
0.106 |
|
|
ORB |
1 |
0.026 |
|
3 |
0.046 |
|
|
SuperPoint |
1 |
0.142 |
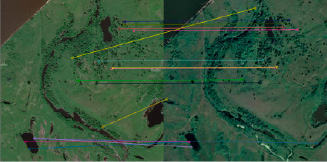
Рис. 3. Пример сопоставления точек с SIFT

Рис. 4. Пример сопоставления точек с ORB

Рис. 5. Пример сопоставления точек с FAST+BRIEF

Рис. 6. Пример сопоставления точек с AKAZE

Рис. 7. Пример сопоставления точек с SuperPoint
Выводы
По результатам видно, что SuperPoint находит больше опорных точек, чем FAST+ BRIEF и SIFT, причем с лучшей точностью и за меньшее время, т.е. превосходит эти методы по всем параметрам. ORB же, требуя меньших вычислительных мощностей, чем SuperPoint, показывает гораздо более низкую точность, что сильно ограничивает его применимость. Быстрое и точное обнаружение и сопоставление опорных точек позволят решать огромный спектр задач, таких как склейка панорамных изображений или обнаружение объектов на изображениях в реальном времени.
Библиографическая ссылка
Нажимова Н.А., Киселев А.А. СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ ОПРЕДЕЛЕНИЯ ОПОРНЫХ ТОЧЕК НА ИЗОБРАЖЕНИЯХ // Научное обозрение. Технические науки. 2024. № 1. С. 23-28;URL: https://science-engineering.ru/ru/article/view?id=1454 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/srts.1454


 science-review.ru
science-review.ru